9th math new book exercise 3.3
9th math new book exercise 3.3 solution
Q1 For A = { 1,2,3,4 } find the following relations in A. State the domain and range of each relation.
(i) { ( x , y ) | y = x }
(ii) { ( x , y ) | y + x = 5 }
(iii) { ( x , y ) | x + y < 5 }
(iv) { ( x , y ) | x + y > 5 }
Solution:-
Fist we’ll find AxA
AxA = { (1,1),(1.2),(1,3),(1,4),(2,1),(2.2),(2,3),(2,4),(3,1),(3.2),(3,3),(3,4),(4,1),(4.2),(4,3),(4,4) }
(i):- { (1,1),(2,2),(3,3),(4,4) }
(ii):- { (1,4),(2,3),(3,2),(4,1) }
(iii):- { (1,1),(1,2),(1,3),(2,1),(2,2),(3,1) }
(iv):- { (2,4),(3,3),(3,4),(4,2),(4,3),(4,4) }
========================================
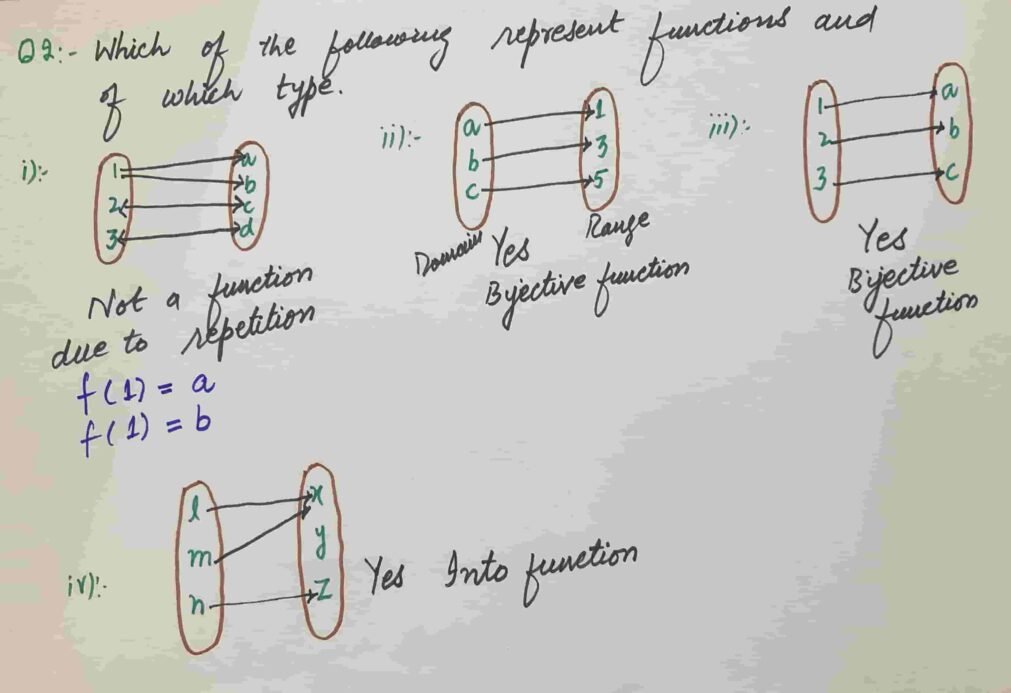
Q2 Which of the following represent functions and of which type
========================================
Q3 If
$$g(x)\;=\;3x+2\\h(x)\;=\;x^2+1$$
then find
(i) g(0)
(ii) g(-3)
(iii) g(2/3)
(iv) h(-1)
(v) h(-4)
(vi) h(-1/2)
Solution:-
(i):-
g(x) = 3x + 2
g(0) = 3(0) + 2
= 0 + 2 = 0
(ii):-
g(x) = 3x + 2
g(-3) = 3(-3) + 2
= -9 + 2 = – 7
(iii):-
g(x) = 3x + 2
g(2/3) = 3(2/3) + 2
= 2 + 2 = 4
(iv):-
$$h(x)\;=\;x^2+1\\\\h(1)\;=\;{(1)}^2+1\\\\=\;1\;+\;1\;=\;2$$
(v):-
$$h(x)\;=\;x^2+1\\\\h(-4)\;=\;{(-4)}^2+1\\\\=\;16\;+\;1\;=\;17$$
(v):-
$$h(x)\;=\;x^2+1\\\\h(\frac{-1}2)\;=\;{(\frac{-1}2)}^2+1\\\\=\;\;\frac14\;+\;1\;\;=\;\;\frac54$$
========================================
Q4 Given that f(x) = a x + b + 1, where a and b are constant numbers. If f(3) = 8 and f(6) = 14, then find the value of a and b.
f(x) = a x + b + 1
f(3) = a(3) + b + 1
f(3) = 3a + b + 1
8 = 3a +b + 1
8 – 1 = 3a + b
7 = 3a + b
3a + b = 7 (i)
f(x) = a x +b + 1
f(6) = a(6) + b + 1
f(6) = 6a + b + 1
14 = 6a + b + 1
14 -1 = 6a + b
13 = 6a + b
6a + b = 13 (ii)
Subtracting eq (ii) from eq (i)
3a + b – 6a – b = 7 – 13
-3a = -6
a = -6/-3
a = 2
Putting a = 2 in equation (i)
3a + b = 7 (i)
3(2) + b = 7
6 + b = 7
b = 7 -6
b = 1
========================================
Q5 Given that g(x) = a x +b + 5 where a and b are constant numbers. If g(-1) = 0 and g(2) = 10, find the values of a and b.
g(x) = a x + b + 5
g(-1) = a (-1) + b + 5
0 = – a + b + 5
a – b = 5 (i)
g(x) = a x +b + 5
g(2) = a (2) +b + 5
10 = 2a + b + 5
10 – 5 = 2a +b
5 = 2a + b
2a + b = 5 (ii)
Adding Eq (i) and (ii)
a -b + 2a + b = 5 + 5
3a = 10
a = 3/10
Putting the value of a in equation (i)
a – b = 5
10/ 3 – b= 5
10/3 – 5 = b
10/3 – 15 = b
-5/3 = b
b = -5/3
======================================
Q6 Consider the following defined by f(x) = 5 x + 1 f(x) = 32, find the value of x.
f(x) = 5x + 1
32 = 5x + 1
32 – 1 = 5x
31 = 5x
31/5 = x
x = 31/5
Q7 Consider the function
$$f(x)\;=c\;x^2+d$$
Where c and d are constant numbers. If f(1) = 6 and f(-2)=10, then find the values of c and d
Solution:-
$$f(x)\;=c\;x^2+d\\\\f(1)\;=\;c{(1)}^2\;+d\\\\6\;=\;c(1)\;+d\\\\c+d=6\;\;(i)$$
$$f(x)\;=c\;x^2+d\\\\f(1)\;=\;c{(-2)}^2\;+d\\\\10\;=\;c(4)\;+d\\\\10\;=4c\;+\;d\\\\4c\;+\;d\;=\;10\;\;(ii)$$
Subtracting equation (i) from equation (ii)
4c+d -(c+d) = 10-6
4c+d-c-d = 4
3c = 4
c = 4/3
Putting the value of c in Equation (i)
6 = c + d
6 = 4/3 + d
d = 6- 4/3
d = 14/3
========================================
Check! Some important links below




