9th class math 2025 chapter 3 notes
9th class math 2025 chapter 3 notes will play a vital role for the preparation of math class 9 because name of new book math class 9 chapter 3 is Sets and Functions. 9th class math 2025 chapter 3 i.e sets is always the key to explore the mainstream of mathematics.
A collection of well defined and distinct objects is called a set.
Are you confused about well defined ?
Let’s try to understand it with the help of an example.
A collection of first five Natural numbers mean { 1,2,3,4,5 }. Hence, its well defined.
But a collection of any five natural numbers is not well defined because we are not completely sure about the numbers. The numbers may or may not be { 1,2,3,4,5 }.
Lets check some important set.
List of Important Sets
Natural Numbers
$$\mathbb{N}\;=\;\{\;1,2,3,4,……….\}$$
Remember that! Other name of Natural numbers is Positive integers.
Whole Numbers
$$\boldsymbol W\;=\;\{\;0,1,2,3,4……….\}$$
Second name of Whole numbers is Non-negative integers.
Integers
$$\mathbb{Z}=\;\{\;0,\pm1,\pm2,\pm3,………\}\\\\OR\\\\\mathbb{Z}\;=\;\{\;….,-3,-2,-1,0,1,2,3,….\}$$
Even Numbers
$$\boldsymbol E=\;\{\;0,\pm2,\pm4,………\}\\\\OR\\\\\boldsymbol E=\;\{\;….,-4,-2,0,2,4,….\}$$
Another name of Even numbers is Even integers.
Odd Numbers
$$\boldsymbol O=\;\{\;\pm1,\pm3,\pm5,……..\}\\\\OR\\\\\boldsymbol O=\;\{\;…,-5,-3,-1,1,3,5….\}$$
We can also say that Odd numbers are actually Odd integers.
Prime Numbers
$$\mathbb{P}=\{\;2,3,5,7,11,13,17,19,23,….\}$$
A prime numbers is a natural number which is greater than 1 and the number itself that has exactly two distinct divisors, 1 and the number itself.
1 is not a prime number.
Composite Numbers
Composite numbers are the numbers which are not prime but keep it in your mind that 1 is neither Prime nor Composite.
Rational numbers
The numbers which can be written in the form of p/q but p and q both must be integers and q will not be 0.
$$\style{font-size:16px}{\mathbb{Q}=\{\;x\vert x=\frac pq\wedge\;p\in\mathbb{Z},q\in\mathbb{Z}\;\&q\neq0\}}$$
first of all fraction must be in its lowest form then check that numerator and denominator must be integers and denominator must not be 0.
Let’s check some examples.
$$\style{font-size:20px}{\frac9{27}\;First\;we\;will\;convert\\it\;in\;its\;lowest\;form\\\frac9{27}\;=\;\frac13\\1\;is\;integer\\3\;is\;integer\\Hence\;\frac13\;is\;rational.}$$
$$\style{font-size:16px}{\frac{\sqrt9}5\;First\;we\;will\;convert\\it\;in\;its\;lowest\;form\\\frac{\sqrt9}5\;=\;\frac35\\3\;is\;integer\\5\;is\;integer\\Hence\;\frac{\sqrt9}5\;is\;rational.}$$
The numbers whose complete square root exist are rational numbers.
$$\style{font-size:16px}{\sqrt1,\sqrt4,\sqrt9,\sqrt{16},\sqrt{25},\sqrt{36},….\\are\;all\;rationals.}$$
In decimal representation if a number stops , its rational and if a number shows pattern after decimal its also rational.
Its mean terminating decimal numbers are rational numbers and non terminating recurring decimal numbers are also rational numbers.
For example 2.5, 0.75, 0.333……., and 0.123123123……. are rational numbers
Irrational numbers
The numbers which are not rational are called irrational numbers.
$$\style{font-size:16px}{Irrational\;numbers\;are\\denoted\;by\;\;\mathbb{Q}’}$$
The numbers whose complete square root does not exist are called irrational numbers.
$$\style{font-size:16px}{\sqrt2,\sqrt3,\sqrt5,\sqrt6,\sqrt7,\sqrt8,….\\are\;all\;irrational\;numbers.}$$.
In decimal representation if a number does not stop and also have NO pattern, is an irrational numbers.
Its mean non terminating non recurring decimal numbers are irrational numbers.
For example 3.14285714285,,,,,,,,,,,,,,,,,,,,,,,, and 2.718281,,,,,,,,,,,,,, are irrational numbers
$$\style{font-size:10px}{\mathrm\pi\;\mathrm{and}\;\mathrm e\;\mathrm{are}\;\mathrm{famous}\;\mathrm{irrational}\;\mathrm{numbers}}$$
Real numbers
All rational and irrational numbers are real numbers.
$$\style{font-size:16px}{\mathbb{R}\;=\;\mathbb{Q}\;\cup\;\mathbb{Q}’}$$
How to represent a set ?
There are three ways to write a set.
Descriptive method:-
A set described in words.
For example, Set of first five Natural numbers.
Tabular method:-
A set described by listing the elements within the brackets.
For example, {1,2,3,4,5}
Set builder notation:-
In set builder notation, we show a set by a symbol or a letter for an arbitrary set member and stating the property common to all the elements.
We can write Set of first five Natural numbers in set builder notation as
$$\style{font-size:20px}{\{\;x\;\vert\;x\;\in\mathbb{N}\;\wedge\;x\;<\;6\;\}\\\\or\\\\{\{\;x\;\vert\;x\;\in\mathbb{N}\;\wedge\;x\;\leq\;5\;\}}\\}$$
Important types of sets:-
Subset:–
If every element of set A is also an element of set B, then A is subset of B and B is called super set of A. A is also called proper subset of B.
$$\style{font-size:20px}{A\;=\;\{\;1,2\;\}\\B\;=\;\{\;1,2,3\;\}\\\\A\;\underline\subset\;B}$$
Equal sets:-
Two set are equal if they have exactly same elements. Second definition is If A is subset of B and B is subset of A, then A=B. These sets are improper sub sets of each other.
$$\style{font-size:20px}{If\;A\;\underline\subset\;B\;and\;B\;\underline\subset\;A\\\\Then\;\;A=B\\}$$
Cardinality of a set:-
Cardinality or cardinal number means number of elements in a set. A = { 1,2,3,4,5 } Cardinality of set A is 5 usually denoted by n(A) = 5.
B={ a,e,i,o,u } Cardinality of set B is also 5 denoted by n(B) =5.
Equivalent sets:-
Two sets are equivalent if they have same number of elements. Second definition is two sets are equivalent if their cardinality is same.
All equal sets are equivalent but its converse may or may not be true..
Universal set:-
A set that contains all the elements under consideration.
Power set:-
Power set contains all the subsets of that set. A = { 1,2,3 }
P(A) = { { }, {1},{2},{3},{1,2},{1,3},{2.3},{1,2,3} }. Because there are three elements in set A, hence its power set will contain 8 elements.
Formula to find the elements of power set is
$$\style{font-size:20px}{Number\;of\;elements\;in\;power\;set\\is\;equal\;to\;2^n\;where\;n\;is\\number\;of\;elements\;of\;that\;set.\\}$$
9th New book Ex3.1
Q1 Write the following sets in set builder notation:
General form:
$$\{\;x\in S\vert condition\;on\;x\}$$
x represents the variable and S represents the set. Condition tells about the properties of the elements.
(i) {1,4,9,16,25,….,484}
$$\{x\vert x=n^2,n\in\mathbb{N}\wedge1\leq n\leq22\}$$
We can also write it as
$$\{x\in\mathbb{N}\;\vert\;x=n^2\wedge1\leq n\leq22\}$$
(ii) {2,4,8,16,32….150}
$$\{x\vert\;x=2^n,n\in\mathbb{N}\;\wedge x\leq150\}$$
{2,4,8,16,32….256}
$$\{x\vert\;x=2^n,n\in\mathbb{N}\;\wedge1\leq n\leq8\}$$
(iii) {-1000,……..-1,0,1,………..,1000}
$$\{x\;\vert\;x\in\mathbb{Z}\;\wedge-1000\leq x\leq1000\}$$
(iv) {6,12,18,….,120}
$$\{x\;\vert\;x\in\mathbb{N}\;\wedge x=6n,-1\leq n\leq20\}$$
(v) {100,102,104,….,400}
$$\{x\vert x\in\boldsymbol E\boldsymbol{\mathit\;}\mathit\wedge\mathit\;\mathit{100}\mathit\;\mathit\leq\mathit\;x\mathit\;\mathit\leq\mathit\;\mathit{400}\mathit\}$$
(vi) {1,3,9,27,81……}
$$\{x\vert x=3^n,n\in\boldsymbol W\boldsymbol{\mathit\;}\mathit\wedge\mathit\;\mathit0\mathit\;\mathit\leq\mathit\;n\mathit\}$$
(vii) {1,2,4,5,10,25,50,100}
$$\{x\;\vert\;x\in\mathbb{N}\;\wedge\;x\;divides\;100\boldsymbol{\mathit\;}\mathit\}$$
We can also write as {x | x is a factor of 100 }
(viii) {5,10,15,….,100}
$$\{x\vert\;x=5n,\;n\in\mathbb{N}\;\wedge\;1\;\leq\;n\;\leq\;20\;\}$$
(ix) The set of all integers from -100 to 100
$$\{x\;\vert\;x\in\mathbb{Z}\;\wedge-100\leq x\leq100\}$$
====================================================================================
Q 2 Write each of the following sets in the tabular form:
(i) $$\{x\vert\;x\;is\;a\;multiple\;of\;3\;\wedge\;x\;\leq\;35\;\}$$
{3,6,9,12,15,18,21,24,27,30,33}
(ii) $$\{x\vert\;x\in\mathbb{R}\;\;\wedge\;2x\;+1=0\;\}$$
2x+1=0
2x=-1
x= -1/2
Hence in tabular form it is {-1/2}
(iii) $$\{x\vert\;x\in\mathbb{P}\;\wedge\;x<\;12\;\}$$
{2,3,5,7,11}
(iv)
{ x | x is a divisor of 128 }
{1,2,4,8,16,32,64,128}
(v) $$\{x\vert\;x=2^n,n\in\mathbb{N}\wedge n<8\}$$
{2,4,8,16,32.64.128}
(vi) $$\{x\vert\;x\in\mathbb{N}\wedge\;x+4\;=\;0\}$$
x+4=0
x=-4 But -4 is not a natural number so set is empty and in tabular form it can be written as { }
(vii) $$\{x\vert\;x\in\mathbb{N}\wedge\;x=x\}$$
{1,2,3,4……………..}
(viii) $$\{x\vert\;x\in\mathbb{Z}\;\wedge\;3x+1\;=\;0\}$$
3x+1 = 0
3x= -1
x = -1/3 But -1/3 is not an integer hence set is empty So in tabular form we will write { }.
====================================================================================
Q3 Write two proper subset of each of the following set:
(i) :- {a, b, c}
{ } , {a} , {b} , {c} ,{a , b} , {a , c} , {b , c} , {a , b , c}
(ii) :- {0 , 1}
{ } , {o} , {1} , {0 , 1}
(iii) :- N
{ } , {1}
(iv) :- Z
{ } , {1}
(v) :- Q
{ } , {1}
(vi) :- R
{ } , {1}
(vii) :- $$\{x\vert x\in\mathbb{Q}\;\wedge0<x\leq2\}$$
{ } , {1}
====================================================================================
Q4 ;- Is there any set which has no proper subset? If so , name that set.
Yes , empty set has no proper subset.
Say A = { }
P (A) = { }
====================================================================================
Q5 :- what is the difference between {a , b} and {(a , b)}?
{ a , b} has two elements ‘a’ and ‘b’.
{(a , b)} has only one element which is {a , b}
====================================================================================
Q6 :- What is the number of element of the power set of each of the following set?
(i) :- { }
Number of element of power set of { } $$2^0\;=\;1$$
(ii) :- {0 , 1}
Number of element of power set {0 , 1} = $$2^2\;=\;4$$
(iii) :- {1 , 2 , 3 , 4 , 5 , 6 , 7}
Number of element of power set {1 , 2 , 3 , 4 , 5 , 6 , 7} = $$2^7\;=\;128$$
(iv) :- {a, {b , c}}
Number of element of power set {a, {b , c}} = $$2^2\;=\;4$$
(v) :- { {a , b} , { b , c} , {d , e} }
Number of element of power set { {a , b} , { b , c} , {d , e} } = $$2^3\;=\;8$$
====================================================================================
Q7 Write down the power set of each of the following sets:
(i)
A = { 9 , 11 }
P(A) = { { } , {9} , {11} , { 9 , 11}}
(ii)
$$B=\;\{\;+\;,\;-,\;\times,\;\div\}$$
$$P\;(B)\;=\;\{\;\{\;\},\{\;+\;\}\;,\;\{-\}\;,\;\{\times\}\;,\;\{\div\}\;,\\\{+\;,\;-\}\;,\;\{+,\;\times\}\;,\;\{+\;,\;\div\}\;,\;\{-\;,\;\times\}\;,\\\{-\;,\;\div\}\;,\;\{\times,\;\div\}\;,\;\{+\;,\;-\;,\;\times\}\;,\\\{\;+\;,\;\times\;,\;\div\}\;,\;\{+,-,\div\},\;\{\;-\;,\;\times,\;\div\;\},\\\{\;+\;,\;-\;,\;\times\;,\;\div\;\}\;\}$$
(iii)
$$C\;=\;\{\;\phi\;\}$$
$$P(C)\;=\{\;\{\;\}\;,\;\{\;\phi\;\}\;\}$$
$$P(C)\;=\{\;\{\;\}\;,\;\{\;\phi\;\}\;\}\;=\;\{\;\{\;\}\;,\;\{\;\{\;\}\;\}\;\}$$
(iv)
D = { a , {b , c} }
P (D) = { { } , {a} , { {b , c} } , { a , {b , c} }
====================================================================================
Operations on Set
Union of two set:-
Union of two sets A and B is the set of all the element which belong two A or B or both.
In Set builder notation
$$A\cup B=\{x\vert x\in A\vee x\in B\vee x\in A\wedge B\}$$
Example:-
A = {1,2} B = {2,3,4} AUB = { 1,2,3,4 }
==========================================
Intersection of two sets:-
Intersection of two sets A and B is the set of all the element which belong to both A and B.
In Set builder notation
$$A\cap B=\;\{\;x\;\vert\;x\in A\;\wedge\;x\in B\;\}$$
Example:-
$$A=\{1,2\}\;\;B=\{2,3,4\}\;\;A\cap B=\{2\}$$
==========================================
Difference of two sets:-
It there are two sets A and B, difference of A to B denoted A-B consists of all the elements belong to A but does not belong to B.
$$A-B\;=\;\{\;x\;\vert\;x\in A\wedge x\not\in B\;\}$$
$$B-A\;=\;\{\;x\;\vert\;x\in B\wedge x\not\in A\;\}$$
Example:-
A = {1,2} B = {2,3,4} A-B = {1} B-A = { 3,4 }
==========================================
Disjoint sets:-
If the intersection of two set is the empty, the sets are called disjoint sets.
A = { 1 , 2 } , B = { 3 , 4 }
$$A\cap B\;=\;\{\;\;\}$$
==========================================
Overlapping Sets:-
If the intersection of two sets is non-empty but neither is a subset of the other.
A = { 1 , 2 } B = { 2 , 3 }
$$A\cap B\;=\;\{\;2\;\}$$
Also, A is not subset of B and B is not subset of A
==========================================
Compliment of a set:-
Compliment of set A is the set of all the element of U, which does not belong to A denoted by $$A^{c\;}\;or\;\;A’$$.
$$A^{c\;}=\;\{x\;\vert\;x\;\in\cup\wedge x\not\in A\}$$
U = { 1 , 2 , 3 , 4 , 5 }
A = { 1 , 2 , 3 }
$$A^c\;=\;\{\;4\;,\;5\;\}$$
==========================================
Exercise 3.2 Math 9th New Book Notes Punjab
Exercise 3.2 Math 9th New Book Notes Punjab board will be completely solved. New Book Notes Punjab Exercise 3.2 Math 9th.
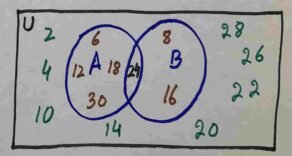
Q1 Consider the universal set
$$U=\{x:x\;is\;multiple\;of\;2\;and\;0<x\leq30\}$$
A= { x:x is a multiple of 6 } and B= { x:x is a multiple of 8 }
(i) :-
List of all elements of sets A and B in tabular form
(ii) $$Find\;A\cap B$$
(iii)
Draw Venn diagram
Solution:-
i)
U = { 2, 4, 6, 8, 10, 11, 12, 14, 16, 18, 20, 22, 24, 26, 28 }
A = { 6, 12, 18, 24, 30 }
B = { 8, 16, 24 }
ii)
$$\;A\cap B\;=\;\{\;24\;\}$$
iii)
Q2 :- Let,
$$U=\{\;x:x\;is\;an\;integer\;and\;0<x\leq150\}$$
$$G=\{x:x\;=2^m\;for\;integer\;m\;and\;0\leq m\leq12\}\;\;$$
$$H=\{\;x:x\;is\;a\;square\;\}$$
(i) :-
List all element of sets G and H in tabular form
(ii) :-
Find GUH
(iii) :- $$Find\;G\cap H$$
Solution:-
i)
G= { 1,2,4,8,16,32,64,128}
H= {1,4,9,16,25,36,49,64,81,100,121,144}
ii)
GUH = {1,2,4,8,9,16,25,32,36,49,64,81,100,121,128,144}
iii)
$$G\cap H=\;\{1,4,16,64\}$$
Q3 Consider the sets
$$P=\{x:x\;is\;a\;prime\;number\;and\;0<x\leq20\}$$
$$Q=\{x:x\;is\;a\;divisor\;of\;210\;and\;0<x\leq20\}$$
(i):-
$$Find\;P\cap Q$$
(ii):-
Find PUQ
Solution:-
P={2,3,5,7,11,13,17,19}
Q={1,2,3,5,6,7,10,14,15}
i)
$$P\cap Q\;=\;\{2,3,5,7\}$$
ii)
$$P\cup Q\;=\;\{1,2,3,5,6,7,10,11,13,14,15,17,19\}$$
Q4 Verify the commutative properties of union and intersection for the following pairs of sets
(i):-
A={1,2,3,4,5}
B={4,6,8,10}
(ii):-
$$\mathbb{N}\;,\;\mathbb{Z}$$
(iii):-
$$A=\{x:x\in\mathbb{R}\wedge x\geq0\}\\B=\;\mathbb{R}\;$$
Solution:-
Commutative property of union
A U B = B U A
Commutative property on intersection
$$A\cap B\;=\;B\cap A$$
i):-
L.H.S = AUB = {1,2,3,4,5} U {4,6,8,10}
= { 1,2,3,4,5,6,8,10 }
R.H.S = BUA = {4,6,8,10} U {1,2,3,4,5}
= {1,2,3,4,5,6,8,10}
L.H.S = R.H.S
$$L.H.S\;=\;A\cap B\\\\=\{1,2,3,4,5\}\cap\{4,6,8,10\}\\=\{4\}$$
$$R.H.S\;=\;B\cap A\\\\=\{4,6,8,10\}\cap\{1,2,3,4,5\}\\=\{4\}$$
ii):-
A= N = {1,2,3,4,….}
B= Z = {0,1,2,3,….}
AUB = NUZ
= {1,2,3,….} U {0,1,2,3,…..}
={0,1,2,3,….} = Z
BUA = ZUN
= {0,1,2,3,….} U {1,2,3,….}
={0,1,2,3,….} = Z
Hence AUB = BUA
$$A\cap B=\;\mathbb{N}\;\cap\;\mathbb{Z}\\=\{1,2,3,…\}\cap\{0,1,2,3,…\}\\=\{1,2,3,….\}\;=\;\mathbb{N}$$
$$B\cap A=\;\mathbb{Z}\cap\mathbb{N}\\=\{0,1,2,3,…\}\cap\{1,2,3,…\}\\=\{1,2,3,….\}\;=\;\mathbb{N}$$
Hence
$$\;A\cap B=B\cap A$$
iii):-
$$A=\{x\vert x\in\mathbb{R}\wedge x\geq0\}\\B=\;\mathbb{R}$$
AUB = R
BUA = R
Hence AUB = BUA
$$A\cap B=\{x\vert x\in\mathbb{R}\wedge x\geq0\}=A\\B\cap A=\{x\vert x\in\mathbb{R}\wedge x\geq0\}=A$$
Hence
$$A\cap B\;=\;B\cap A$$
Q5 Let U={a,b,c,d,e,f,g,h,i,j} A={a,b,c,d,g,h} B={c,d,e,f,j} Verify De Morgan’s Laws for these sets. Draw Venn diagram
Solution:-
$$(\;A\cup B\;)’=A’\cap B’\\(\;A\cap B\;)’=A’\cup B’$$
Lets check $$(\;A\cup B\;)’=A’\cap B’$$
AUB = { a, b, c, d, g, h } U { c, d, e, f, j }
= { a, b, c, d, e, f, g, h, j, }
(AUB)’ = U – (AUB)
= { a, b, c, d, e, f, g, h, i, j } – {a, b, c, d, e, f, g, ,h, j }
= { i }
L. H. S = { i }
A’ = U – A
= { a, b, , c, d, e, f, g, h, i, j } – { a, b, c, d, g, h }
={ e, f, i, j }
B’ = U – B
= { a, b, c, d, e, f, g, h, i, j } – { c, d, e, f, j }
= { a, b, g, h, i }
$$\;A’\cap B’$$
= { e, f, i, j } – { a, b, g, h, i }
= { i }
R.H.S = { i }
Hence L.H.S = R.H.S
========================================
Lets Check $$(\;A\cap B\;)’=A’\cup B’$$
$$A\cap B=\{a,b,c,d,g,h\}\cap\{c.d.e.f.j\}\\=\{c,d\}$$
$$(A\cap B)’=U-(A\cap B)$$
= { a, b, c, d, e, f, g, h, i, j } – { c, d }
= { a, b, e, f, g, h, i, j }
L. H. S = { a, b, e, f, g, h, i, j }
A’ = U – A
= { a, b, c, d, e, f, g, h, i, j } – { a, b, c, d, g, h }
= { e, f, i, g }
B’ = U – B
= { a, b, c, d, e, f, g, h, i, j } – { c, d, e, f, j }
= { a, b, g, h, i }
A’ U B’
= { e, f, i, j } – { a, b, g, h, i }
= { a, b, e, f, g, h, i, j }
R.H.S = { a, b, e, f, g, h, i, j }
Hence L.H.S = R.H.S
========================================
Lets draw Venn diagrams
For Venn diagram check the following video
Q6 Let U = { 1,2,3,….,20 } A={1,3,5,….,19} Verify the following
$$(i)\;\;A\cup A’=\cup\;\;(ii)\;A\cap U=\;A\\(iii)\;A\cap A’\;=\;\{\;\}\;$$
Solution:-
A’ =U – A = {1,2,3,…,20} – {1,3,5,….,19} ={2,4,6,…,20}
(i)
L.H.S = AUA’ ={1,3,5,…,19} U {2,4,6,…,20}
={1,2,3,…,20}=U
=R.H.S
(ii)
$$L.H.S\;=\;A\cap U\\=\{1,3,5,…,19\}\cap\{\{1,2,3,…,20\}$$
={1,3,5,…,19}=A
=R.H.S
(iii)
$$L.H.S\;=\;A\cap A’\\=\{1,3,5,…,19\}\cap\{\{2,4,6,…,20\}$$
= { }
=R.H.S
Q7 In a class of 55 students, 34 like to play cricket and 30 like to play hockey. Also each student likes to play at least one of the two games. How many students like to play both games ?
Solution:-
|HUC| = 55 |H| = 30 |C| = 34
Principle of inclusion and exclusion for two sets
$$\vert H\cup C\vert=\vert H\vert\;+\;\vert C\vert\;-\vert H\cap C\vert$$
$$\vert H\cap C\vert=\vert H\vert\;+\;\vert C\vert\;-\vert H\cup C\vert\\\vert H\cap C\vert=30+34-55=9\\$$
Q8 In a group of 500 employees, 250 can speak Urdu , 150 can speak English, 50 can speak Punjabi, 40 can speak Urdu and English, 30 can speak both English and Punjabi, and 10 can speak Urdu and Punjabi. How many can speak all three languages ?
|U| = 250 |E| = 150 |P| 50
$$\vert U\cap E\vert=40,\;\vert E\cap P\vert=30,\;\vert U\cap P\vert=10\\\vert E\cup U\cup P\vert=500,\;\;\vert E\cap U\cap p\vert=?\\$$
Principle of Inclusion and exclusion for three sets
$$\vert E\cup U\cup P\vert=\vert U\vert+\vert E\vert+\vert P\vert\\-\vert U\cap E\vert-\vert E\cap P\vert-\vert U\cap P\\+\vert E\cap U\cap P\vert\\After\;putting\;the\;values\\\\500=250+150+50-40-30\\-10+\vert E\cap U\cap P\vert\\\\Hence\\\\130\;=\;\vert E\cap U\cap P\vert\\\\$$
Q9 In sport events, 19 people wear blue shirts, 15 wear green shirts, 3 wear blue and green shirts, 4 wear a cap and blue shirts, and 2 wear a cap and green shirts, The total number of people with either a blue or green shirt or cap is 25. How many people are wearing caps?
|B|= 19, |G|= 15, |C|= ?
$$\vert G\cap B\vert=3\\$$ $$\vert C\cap B\vert=4,\;\vert C\cap G\vert=2\\\vert B\cup G\cup C\vert\;=\;?\\\\$$
$$\vert B\cup G\cup C\vert\\=\vert B\vert+\vert G\vert+\vert C\vert-\vert B\cap G\vert\\-\vert C\cap B\vert-\vert C\cap G\vert+\vert B\cap G\cap C\vert\\\\$$
Principle of inclusion and exclusion
$$\vert B\cup G\cup C\vert=\vert B\vert+\vert G\vert+\vert C\vert\\-\vert B\cap G\vert-\vert C\cap B\vert-\vert C\cap G\vert+\vert B\cap G\cap C\vert\\\\$$
After putting the values, we get
25 = 19+ 15+ |C|- 3- 4- 2+ 0
25- 19- 15+ 3+ 4+ 2= |C|
|C| = 0
Q9 In sport events, 10 people wear blue shirts, 15 wear green shirts, 3 wear blue and green shirts, 4 wear a cap and blue shirts, and 2 wear a cap and green shirts, The total number of people with either a blue or green shirt or cap is 25. How many people are wearing caps?
|B|= 10, |G|= 15, |C|= ?
$$\vert G\cap B\vert=3\\$$ $$\vert C\cap B\vert=4,\;\vert C\cap G\vert=2\\\vert B\cup G\cup C\vert\;=\;?\\\\$$
$$\vert B\cup G\cup C\vert\\=\vert B\vert+\vert G\vert+\vert C\vert-\vert B\cap G\vert\\-\vert C\cap B\vert-\vert C\cap G\vert+\vert B\cap G\cap C\vert\\\\$$
Principle of inclusion and exclusion
$$\vert B\cup G\cup C\vert=\vert B\vert+\vert G\vert+\vert C\vert\\-\vert B\cap G\vert-\vert C\cap B\vert-\vert C\cap G\vert+\vert B\cap G\cap C\vert\\\\$$
After putting the values, we get
25 = 10+ 15+ |C|- 3- 4- 2+ 0
25- 10- 15+ 3+ 4+ 2= |C|
|C| = 9
Q9 In sport events, 19 people wear blue shirts, 15 wear green shirts, 3 wear blue and green shirts, 4 wear a cap and blue shirts, and 2 wear a cap and green shirts, The total number of people with either a blue or green shirt or cap is 34. How many people are wearing caps?
|B|= 19, |G|= 15, |C|= ?
$$\vert G\cap B\vert=3\\$$ $$\vert C\cap B\vert=4,\;\vert C\cap G\vert=2\\\vert B\cup G\cup C\vert\;=\;?\\\\$$
$$\vert B\cup G\cup C\vert\\=\vert B\vert+\vert G\vert+\vert C\vert-\vert B\cap G\vert\\-\vert C\cap B\vert-\vert C\cap G\vert+\vert B\cap G\cap C\vert\\\\$$
Principle of inclusion and exclusion
$$\vert B\cup G\cup C\vert=\vert B\vert+\vert G\vert+\vert C\vert\\-\vert B\cap G\vert-\vert C\cap B\vert-\vert C\cap G\vert+\vert B\cap G\cap C\vert\\\\$$
After putting the values, we get
34 = 10+ 15+ |C|- 3- 4- 2+ 0
34- 10- 15+ 3+ 4+ 2= |C|
|C| = 9
Q10 In a training session, 17 participants have laptops, 11 have tablets, 9 have laptops and tablets, 6 have laptops and books, and 4 have both tablets and books. eight participants have all three items. The total number of participants with laptops, tablets, or books is 35. How many participant have books?
|L|= 17, |T|= 11, |B|= ?
$$\vert L\cap T\vert=9,\;\vert L\cap B\vert=6\;\vert T\cap B\vert=4\;\\\vert L\cap T\cap B\vert=8\\\\$$
| L U T U B | = 35
Principle of inclusion and exclusion
$$\vert LUTUB\vert=\vert L\vert+\vert T\vert+\vert B\vert\\-\vert L\cap T\vert-\vert L\cap B\vert-\vert T\cap B\vert+\vert L\cap T\cap B\vert\\\\$$
35 = 17+ 11+ |B|- 9- 9- 4+ 8
35 = 36- 19+ |B|
|B| = 18
Q11 A shopping mall has 150 employees labelled 1 to 150, representing the Universal set U. The employees fall into the following categories;
- Set A: 40 employees with a salary range of 30K-45K, labelled from 50 to 89.
- Set B: 50 employees with a salary range of 50K-80K, labelled from 101 to 150.
- Set C: 60 employees with a salary range of 100K-150K, labelled from 1 to 49 and 90 to 100.
$$(a)\;Find\;(\;A’UB’)\;\cap C\;\\\;(a)\;Find\;n\{\;A\cap(B’\cap C’\;)\;\}\;\\\\$$
Solution:-
A’ = All labels except 50 to 89
= { 1, 2, 3, . . . . 49, 90, 91, . . . . 150 }
B’ = All labels except 101 to 150 }
= {1, 2, 3, . . . . 100 }
(a):-
A’UB’ = { 1, 2, 3, . . . . 49, 90, 91, . . . . 150 } U {1, 2, 3, . . . . 100 }
= { 1,2,3,4,…..150 }
$$(A’\cup B’)\cap C\\=\{1,2,3,…,150\}\cap\{1,2,3,…,49,90,91,…,100\}\\=\{1,2,3,…..,150\}\\\\$$
(b):-
B’ = {1,2,3…,100} C’ = {50,51,52,…,89,101,101,…,150}
$$B’\cap C’\\=\{1,2,3,…,100\}\cap\{50,51,52,…,89,101,…,150\}\\=\{\;50,51,52,……..,89\;\}\\\\$$
$$A\cap(B’\cap C’)\\=\{50,51,52,…,89\}\cap\{50,51,52,…,89\}\\=\{50,51,52,…,89\}\;=\;A\\\\$$
$$Hence\\n\{A\cap(B’\cap C’)\}\;=\;40\\\\$$
Q12 In a school with 1 25 students participants in at least one of the following sports: cricket, football, or hockey.
- 60 students play cricket.
- 70 students play football.
- 40 students play hockey.
- 25 students play both cricket and football.
- 15 students play both football and hockey.
- 10 students play both cricket and hockey.
(a) How many students play all three sports?
(b) Draw a Venn diagram showing the distribution of sports participation in all games.
Solution:-
(a):-
| C | = 60, | F |= 70, | H | = 40
$$\vert C\cap F\vert=25,\;\vert F\cap H\vert=15,\;\vert C\cap H\vert=10\\\\\vert C\cup F\cup H\vert\;=\;125,\;\vert C\cap F\cap H\vert\;=\;?$$
Principle of Inclusion and Exclusion for three sets
$$\vert C\cup F\cup H\vert=\vert C\vert+\vert F\vert+\vert H\vert-\vert C\cap F\vert\\-\vert F\cap H\vert-\vert C\cap H\vert+\vert C\cap F\cap H\vert$$
After putting the value , we get
$$125=60+70+40-25\\-15-10\;+\;\vert C\cap F\cap H\vert$$
$$\vert C\cap F\cap H\vert\;=\;5$$
(b):- For Venn Diagram click on the following link
Q13 A survey was conducted in which 130 people were asked about their favourite foods. The survey results showed the following information:
- 40 people said they liked nihari.
- 65 people said they liked biryani.
- 50 people said they liked korma.
- 20 people said they liked nihari and biryani.
- 35 people said they liked biryani and korma.
- 27 people said they liked nihari and korma.
- 12 people said they liked all three foods nihari, biryani, and korma.
(a) At least how many people like nihari, biryani or korma?
(b) How many people did not like nihari, biryani or korma?
(c) How many people like only one of the following foods: nihari, biryani, or korma?
(d) Draw a Venn diagram.
Solution:-
(a):-
|N| = 40, |B| = 65, |K| = 50, |NUBUK| = ?
$$\vert N\cap B\vert=20,\;\;\vert B\cap K\vert=35,\;\\\\\vert N\cap K\vert=27,\;\;\vert N\cap B\cap K\vert=12$$
Principle of inclusion and exclusion
$$\vert N\cup B\cup K\vert=\vert N\vert+\vert B\vert+\vert K\vert\\-\vert N\cap B\vert-\vert N\cap K\vert-\vert B\cap K\vert\\+\vert N\cap B\cap K\vert$$
After putting the values we get
$$\vert N\cup B\cup K\vert=40+65+50\\-20-27-35+12$$
$$\vert N\cup B\cup K\vert\;=\;85$$
(b):-
People who didn’t like Nihari, Biryani or Korma = 130-85 = 45
(c):-
People who like only Nihari
$$=\vert N\vert-\vert N\cap B\vert-\vert N\cap K\vert+\vert N\cap B\cap K\vert$$
= 40 – 20 – 27 + 12 = 5
People who like only Biryani
$$=\vert B\vert-\vert K\cap B\vert-\vert N\cap B\vert+\vert N\cap B\cap K\vert$$
= 65 – 35 – 20 + 12 = 22
People who like only Korma
$$=\vert K\vert-\vert K\cap B\vert-\vert N\cap K\vert+\vert N\cap B\cap K\vert$$
= 50 – 35 – 27 + 12 = 0
People who like only one of the food = 5 + 22 + 0 = 27
(d):-
For Venn Diagram click on the following link
9th math new book exercise 3.3
9th math new book exercise 3.3 solution
Q1 For A = { 1,2,3,4 } find the following relations in A. State the domain and range of each relation.
(i) { ( x , y ) | y = x }
(ii) { ( x , y ) | y + x = 5 }
(iii) { ( x , y ) | x + y < 5 }
(iv) { ( x , y ) | x + y > 5 }
Solution:-
Fist we’ll find AxA
AxA = { (1,1),(1.2),(1,3),(1,4),(2,1),(2.2),(2,3),(2,4),(3,1),(3.2),(3,3),(3,4),(4,1),(4.2),(4,3),(4,4) }
(i):- { (1,1),(2,2),(3,3),(4,4) }
(ii):- { (1,4),(2,3),(3,2),(4,1) }
(iii):- { (1,1),(1,2),(1,3),(2,1),(2,2),(3,1) }
(iv):- { (2,4),(3,3),(3,4),(4,2),(4,3),(4,4) }
========================================
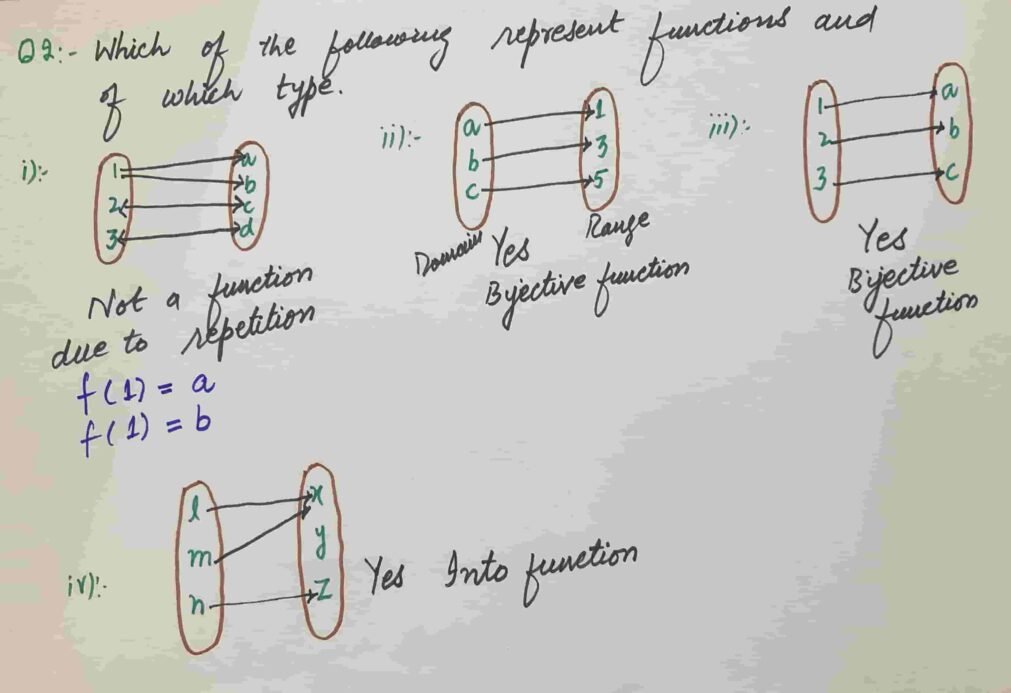
Q2 Which of the following represent functions and of which type
========================================
Q3 If
$$g(x)\;=\;3x+2\\h(x)\;=\;x^2+1$$
then find
(i) g(0)
(ii) g(-3)
(iii) g(2/3)
(iv) h(-1)
(v) h(-4)
(vi) h(-1/2)
Solution:-
(i):-
g(x) = 3x + 2
g(0) = 3(0) + 2
= 0 + 2 = 0
(ii):-
g(x) = 3x + 2
g(-3) = 3(-3) + 2
= -9 + 2 = – 7
(iii):-
g(x) = 3x + 2
g(2/3) = 3(2/3) + 2
= 2 + 2 = 4
(iv):-
$$h(x)\;=\;x^2+1\\\\h(1)\;=\;{(1)}^2+1\\\\=\;1\;+\;1\;=\;2$$
(v):-
$$h(x)\;=\;x^2+1\\\\h(-4)\;=\;{(-4)}^2+1\\\\=\;16\;+\;1\;=\;17$$
(v):-
$$h(x)\;=\;x^2+1\\\\h(\frac{-1}2)\;=\;{(\frac{-1}2)}^2+1\\\\=\;\;\frac14\;+\;1\;\;=\;\;\frac54$$
========================================
Q4 Given that f(x) = a x + b + 1, where a and b are constant numbers. If f(3) = 8 and f(6) = 14, then find the value of a and b.
f(x) = a x + b + 1
f(3) = a(3) + b + 1
f(3) = 3a + b + 1
8 = 3a +b + 1
8 – 1 = 3a + b
7 = 3a + b
3a + b = 7 (i)
f(x) = a x +b + 1
f(6) = a(6) + b + 1
f(6) = 6a + b + 1
14 = 6a + b + 1
14 -1 = 6a + b
13 = 6a + b
6a + b = 13 (ii)
Subtracting eq (ii) from eq (i)
3a + b – 6a – b = 7 – 13
-3a = -6
a = -6/-3
a = 2
Putting a = 2 in equation (i)
3a + b = 7 (i)
3(2) + b = 7
6 + b = 7
b = 7 -6
b = 1
========================================
Q5 Given that g(x) = a x +b + 5 where a and b are constant numbers. If g(-1) = 0 and g(2) = 10, find the values of a and b.
g(x) = a x + b + 5
g(-1) = a (-1) + b + 5
0 = – a + b + 5
a – b = 5 (i)
g(x) = a x +b + 5
g(2) = a (2) +b + 5
10 = 2a + b + 5
10 – 5 = 2a +b
5 = 2a + b
2a + b = 5 (ii)
Adding Eq (i) and (ii)
a -b + 2a + b = 5 + 5
3a = 10
a = 3/10
Putting the value of a in equation (i)
a – b = 5
10/ 3 – b= 5
10/3 – 5 = b
10/3 – 15 = b
-5/3 = b
b = -5/3
======================================
Q6 Consider the following defined by f(x) = 5 x + 1 f(x) = 32, find the value of x.
f(x) = 5x + 1
32 = 5x + 1
32 – 1 = 5x
31 = 5x
31/5 = x
x = 31/5
Q7 Consider the function
$$f(x)\;=c\;x^2+d$$
Where c and d are constant numbers. If f(1) = 6 and f(-2)=10, then find the values of c and d
Solution:-
$$f(x)\;=c\;x^2+d\\\\f(1)\;=\;c{(1)}^2\;+d\\\\6\;=\;c(1)\;+d\\\\c+d=6\;\;(i)$$
$$f(x)\;=c\;x^2+d\\\\f(1)\;=\;c{(-2)}^2\;+d\\\\10\;=\;c(4)\;+d\\\\10\;=4c\;+\;d\\\\4c\;+\;d\;=\;10\;\;(ii)$$
Subtracting equation (i) from equation (ii)
4c+d -(c+d) = 10-6
4c+d-c-d = 4
3c = 4
c = 4/3
Putting the value of c in Equation (i)
6 = c + d
6 = 4/3 + d
d = 6- 4/3
d = 14/3
========================================
Check! Some important links below
Math 9th chapter 1 real numbers notes
For You tube video 9th class math 2025 chapter 3
To check Math 9th new book review exercise chapter 2
For Math 9th new book review exercise chapter 1
For Home page Notespunjab.com




