9th Class Physics 2025 Numerical

9th Class Physics 2025 Numerical solution

Smart Syllabus 9th class physics Chapter 1 Numerical

1.1  Calculate the number of seconds in a (a) day (b) week (c) month and state you answer using SI Prefixes.

Number of minutes in 1 hour = 60

Seconds in 1 hour = (60) (60) = 3600

Seconds in 1 day = (3600) (24) = 86,400

$$=(\frac{86400}{1000})\;(1000)s\\\\=(86.4)\;(1000)s\\\\=86.4\;Ks\\$$

Number of seconds in a week = (86,400) (7)

= 604,800

$$=(\frac{604800}{1000})\;(1000)s\\\\=(604.8)\;(1000)s\\\\=604.8\;Ks\\$$

Number of seconds in 1 month = (86,400) (30)

= 2,592,000

$$=(\frac{2592000}{1000000})\;(1000000)s\\\\=(2.592)\;(1000000)s\\\\=2.592\;Ms\\$$

==============================

1.3  Solve the following addition or subtraction. State your answer in scientific notation

$$(a)\;\;4\times10^{-4}kg\;+3\times10^{-5}kg\\\\=\;10^{-4}(4\;+\;3\times10^{-1}\;)\;kg\\\\=\;10^{-4}(4\;+\;\frac3{10}\;)\;kg\\\\=\;10^{-4}(4\;+\;0.3)\;kg\\\\=\;10^{-4}(4.3\;)\;kg\\\\=\;4.3\;\times10^{-4}\;kg\\\\\\(b)\;\;5.4\times10^{-6}\;m\;-\;3.2\times10^{-5}\;m\\\\=\;10^{-5}(5.4\;\times10^{-1}-3.2)m\\\\=\;10^{-5}(\frac{5.4}{10}-3.2)m\\\\=\;10^{-5}(0.54-3.2)m\\\\=\;10^{-5}(-2.66)m\\\\=\;-2.66\;\times10^{-5}m\\\\\\\\\\$$

===============================

1.4  Solve the following multiplication or division. State your answer in scientific notation.

$$(a)\;\;\;(5\times10^4m)\;\times\;(3\times10^{-2}m)\\(b)\;\;\;\frac{6\times10^8kg}{3\times10^4\;m^3}\;\\$$

$$(a)\;\;\;(5\times10^4m)\;\times\;(3\times10^{-2}m)\\\\=\;\;5\times3\times10^4\times10^{-2}\times m\times m\\\\=\;15\times10^{4-2}\;\times m^2\\\\=\;15\times10^2\;m^2\\\\=\;1.5\;\times10^1\;\times10^2\;m^2\\\\=\;1.5\;\times10^{1+2}m^2\\\\=\;1.5\;\times10^3m^2\\\\\\(b)\;\;\;\frac{6\times10^8kg}{3\times10^4\;m^3}\;\\=\;2\times10^8\times10^{-4}\;kg\;m^{-3}\\\\=\;2\times{(10)}^{8-4}\;kg\;m^{-3}\\\\=\;2\times10^4\;kg\;m^{-3}\\\\$$

===============================

1.6  State the number of significant  digits in each measurement.

$$(a)\;0.0045m\;\;(b)\;2.047m\;\\(c)\;3.40m\;\;(d)\;3.420\;\times\;10^4m\\\\(a)\;0.0045m\\All\mathit\;non\mathit\;zero\mathit\;digits\mathit\;are\mathit\;significant\mathit.\\Zeros\;are\;not\;significant\;here.\;\\4\;and\;5\;are\;significant.\\Hence,\;there\;are\;only\;2\;\\significant\;figures.\\\\(b)\;2.047m\\All\mathit\;non\mathit\;zero\mathit\;digits\mathit\;are\mathit\;significant\mathit.\;\\Zero\;between\;non\;zeros\;are\\significant.\;\\All\;the\;digits\;are\;significant\;here.\\So,\;there\;are\;4\;significant\;figures.\\\\c)\;3.40m\\All\mathit\;non\mathit\;zero\mathit\;digits\mathit\;are\mathit\;significant\mathit.\\Zero\;after\;the\;decimical\;point\;is\\significant.\;Hence,\;there\;are\;3\\significant\;figures.\\\\(d)\;3.420\;\times\;10^4m\\All\mathit\;non\mathit\;zero\mathit\;digits\mathit\;are\mathit\;significant\mathit.\\Zero\;after\;the\;decimical\;point\\is\;significant.\;Hence,\;there\;are\\4\;significant\;figures.$$

================================

1.8  Write using correct prefixes

$$\boldsymbol(\boldsymbol a\boldsymbol)\boldsymbol\;\boldsymbol\;\mathbf5\boldsymbol.\mathbf0\boldsymbol\;\boldsymbol\times\boldsymbol\;\mathbf{10}^{\mathbf4}\boldsymbol\;\boldsymbol c\boldsymbol m\\\\=\;5.0\;\times\;10^4\;\times\;10^{-2}m\\\\=\;5.0\;\times\;10^{4-2}m\\\\=5.0\;\times\;10^2m\\\\=\;\frac{5.0\;\times\;10^2km}{1000}\\\\=\;\frac{5.0\;\times\;100\;km}{1000}\\\\=\;\frac{500\;km}{1000}\\\\=\;0.5\;km\\\\\boldsymbol(\boldsymbol b\boldsymbol)\boldsymbol\;\boldsymbol\;\mathbf{580}\boldsymbol\;\boldsymbol\times\boldsymbol\;\mathbf{10}^{\mathbf2}\boldsymbol\;\boldsymbol g\\\\=\frac{\;580\;\times\;10^2\;kg}{1000}\\\\=\;\frac{\;580\;\times\;100\;kg}{1000}\\\\=\;58\;kg\\\\\boldsymbol(\boldsymbol c\boldsymbol)\boldsymbol\;\boldsymbol\;\mathbf{45}\boldsymbol\;\boldsymbol\times\boldsymbol\;\mathbf{10}^{\boldsymbol-\mathbf4}\boldsymbol\;\boldsymbol s\\\\=\;45\;\times\;10^{-4}\;\times\;1000\;\;ms\\\\=\;\frac{45\;\;\times\;1000\;\;ms}{10^4}\\\\=\;\frac{\;45000\;\;ms}{10000}\\\\=\;4.5\;ms\\\\$$

===============================

1.10

$$Express\;the\;density\\of\;mercury\;given\;as\\13.6\;g\;c\;m^{-3}\;in\;kg\;m^{-3}\\\\\\$$

$$13.6\;g\;c\;m^{-3}\\\\=\;\frac{13.6\;\;kg\;c\;m^{-3}}{1000}\\\\=\;0.0136\;\;kg\;c\;m^{-3}\\\\\mathbf1\boldsymbol\;\boldsymbol c\boldsymbol m\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{10}^{\boldsymbol-\mathbf2}\boldsymbol\;\boldsymbol m\\\\\mathbf1\boldsymbol\;\boldsymbol c\boldsymbol\;\boldsymbol m^{\mathbf3}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{10}^{\boldsymbol-\mathbf6}\boldsymbol\;\boldsymbol m^{\mathbf3}\\\\\;0.0136\;\;kg\;c\;m^{-3}\\\\=\frac{0.0136\;kg}{\;c\;m^3}\\\\=\;\frac{0.0136\;kg}{\;10^{-6}\;m^3}\\\\=0.0136\;\times10^6\;\;kg\;\;\;m^{-3}\\\\=\;1.36\;\times\;10^{-2\;}\times10^6\;\;kg\;\;\;m^{-3}\\\\=\;1.36\;\times10^{-2+6}\;\;kg\;\;\;m^{-3}\\\\=\;1.36\;\times10^4\;\;kg\;\;\;m^{-3}\\\\$$

===============================

Smart Syllabus 9th class physics Chapter 2 Numerical

 

$$2.1\;\;Draw\;the\;\\representative\;line\;of\\the\;following\;vectors:\\(a)\;A\;velocity\;of\\400\;m\;s^{-1}\;making\;an\\angle\;of\;60\;degree\\with\;x-axis.\\(b)\;A\;force\;of\;50\;N\\making\;an\;angle\;of\\120^\circ\;\;with\;x-axis.$$

==================================

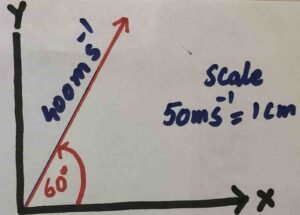
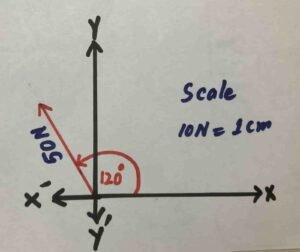
$$2.2\;\;\;A\;car\;is\;moving\\with\;an\;average\;speed\\of\;72\;km\;h^{-1}.\;\;How\\much\;time\;will\;it\\take\;to\;cover\;a\\dis\tan ce\;of\;360\;km\;?$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Average\mathit\;speed\mathit\;\mathit=\mathit\;v_{\mathit a\mathit v}\mathit=\mathit\;\mathit{72}\mathit\;km\mathit\;h^{\mathit-\mathit1}\\Distance\mathit\;\mathit=\mathit\;S\mathit\;\mathit=\mathit\;\mathit{360}\mathit\;km\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\;S\;=\;v_{av}\;\times\;t\\\\\mathit{360}\mathit\;km\mathit\;\mathit=\mathit\;\mathit{72}\mathit\;km\mathit\;h^{\mathit-\mathit1}\mathit\;\mathit\times\mathit\;t\\\frac{\mathit{360}\mathit\;\mathit k\mathit m}{\mathit{72}\mathit\;\mathit k\mathit m\mathit\;\mathit h^{\mathit-\mathit1}}\mathit\;\mathit=\mathit\;t\\\mathit5\mathit\;h\mathit\;\mathit=\mathit\;t\\t\mathit\;\mathit=\mathit\;\mathit5\mathit\;h\\$$

t=5 x 60= 300 min =300 x 60s= 18000 s

==================================

$$2.3\;\;\;A\;truck\;starts\\from\;rest.\;It\;reaches\\a\;velocity\;of\;90\;km\;h^{-1}\\in\;50\;seconds.\;Find\\its\;average\;acceleration.\\$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit{90}\mathit\;km\mathit\;h^{\mathit-\mathit1}\\\\\mathit=\mathit\;\mathit{90}\mathit\;\mathit\times\mathit\;\frac{\mathit{1000}}{\mathit{3600}}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;\mathit{90}\mathit\;\mathit\times\mathit\;\mathit0\mathit.\mathit{277}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\\\\mathit\;\mathit=\mathit\;\mathit{24}\mathit.\mathit{93}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit{50}\mathit\;seconds\\\\Average\mathit\;acceleration\mathit\;\mathit=\mathit\;a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol\;\boldsymbol:\boldsymbol-\\a_{av}\;=\;\;\frac{v_f\;-\;v_i}t\\\\a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit\;\frac{\mathit\;\mathit{24}\mathit.\mathit{93}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}\mathit\;\mathit\;\mathit-\mathit\;\mathit0\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}}{\mathit{50}\mathit\;\mathit s}\\\\a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit\;\frac{\mathit\;\mathit{24}\mathit.\mathit{93}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}}{\mathit{50}\mathit\;\mathit s}\\\\a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit0\mathit.\mathit{498}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit0\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\\\\\\\\\$$

==================================

$$2.4\;\;A\;car\;passes\;a\\green\;traffic\;signal\\while\;moving\;with\;a\\velocity\;of\;5\;m\;s^{-1}.\\It\;then\;accelerates\;to\\1.5\;m\;s^{-2}.\;What\;is\;the\\velocity\;of\;car\;after\\5\;seconds?$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Acceleration\mathit\;\mathit=\mathit\;a\mathit\;\mathit=\mathit\;\mathit1\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit5\mathit\;seconds\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\v_f\;=\;v_i\;+\;at\\\\v_{\mathit f}\mathit=\mathit\;\mathit\;\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit+\mathit\;\mathit1\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit\;\mathit(\mathit5\mathit\;s\mathit)\\\\v_{\mathit f}\mathit=\mathit\;\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit+\mathit\;\mathit7\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\\\v_{\mathit f}\mathit=\mathit\;\mathit{12}\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\\\\\\\\\$$

==================================

$$2.6\;\;A\;wagon\;is\\moving\;on\;a\;road\\with\;a\;velocity\\of\;54\;km\;h^{-1}.\\Brakes\;are\;applied\\suddenly.\;The\;wagon\\covers\;a\;dis\tan ce\;of\\25\;m\;before\;stopping.\\Determine\;the\;\\acceleration\;of\;the\\wagon.$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit{54}\mathit\;km\mathit\;h^{\mathit-\mathit1}\\\\\mathit=\mathit{54}\mathit\;\mathit\times\mathit\;\frac{\mathit{1000}}{\mathit{3600}}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;\mathit{54}\mathit\;\mathit\times\mathit\;\mathit0\mathit.\mathit{278}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\mathit=\mathit\;\mathit{15}\mathit.\mathit{012}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Distance\mathit\;\mathit=\mathit\;S\mathit\;\mathit=\mathit\;\mathit{25}\mathit\;m\\\\Acceleration\mathit\;\mathit=\mathit\;a\mathit\;\mathit=\mathit\;\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\mathbf2\boldsymbol a\boldsymbol S\boldsymbol\;\boldsymbol=\boldsymbol\;{\mathbf v}_{\mathbf f}^{\mathbf2}\boldsymbol\;\boldsymbol-\boldsymbol\;{\mathbf v}_{\mathbf i}^{\mathbf2}\\\\\mathit2a\mathit(\mathit{25}m\mathit)\mathit\;\mathit=\mathit\;\mathit0^{\mathit2}\mathit\;\mathit-\mathit\;{\mathit(\mathit{15}\mathit.\mathit{012}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit)}^{\mathit2}\\\\a\mathit\;\mathit=\mathit\;\frac{\mathit-\mathit{225}\mathit.\mathit{36}\mathit\;\mathit m^{\mathit2}\mathit\;\mathit s^{\mathit-\mathit2}}{\mathit{50}\mathit m}\\\\a\mathit\;\mathit=\mathit\;\mathit-\mathit4\mathit.\mathit{507}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\$$

==================================

$$2.7\;\;\;\;A\;stone\;is\\dropped\;from\;a\\height\;of\;45\;m.\\How\;long\;will\;it\\take\;to\;reach\;the\\ground\;?\;What\;will\\be\;its\;velocity\;just\\before\;hitting\;the\\ground\;?$$

$$height\;=\;h\;=\;45\;m\\Initial\;velocity\;=\;v_i=\;0\;ms^{-1}\\Time\;=\;t\;=\;?\\Final\;velocity\;=\;v_f\;=\;?\\Gravitational\;acceleration=g=9.8ms^{-2}$$

Lets calculate the time first with the help of 2nd equation of motion.

$$h=v_it\;+\;\frac12gt^2\\45m=0(t)\;+\frac12(10ms^{-2})\;t^2\\\frac{45m}{5ms^{-2}}\;=\;t^2\\t^2\;=\;9\;s^2\\t\;=\;3s\\$$

Lets calculate final velocity with the help of 1st equation of motion

$$v_f\;=\;v_i\;+\;a\;t\\v_f\;=\;0\;+(10ms^{-2})\;(\;3\;s)\\v_f\;=\;30\;m\;s^{-1}\\$$

==================================

$$2.9\;\;A\;ball\;is\;dropped\\from\;the\;top\;of\;a\\tower.\;The\;ball\\reaches\;the\;ground\\in\;5\;seconds.\;Find\\height\;of\;the\;tower\;\\and\;velocity\;of\;the\\ball\;with\;which\;it\\strikes\;the\;ground.\;$$

$$\;Data:-\boldsymbol\;\\\\Time\mathit\;\mathit=\mathit\;\mathit5\mathit\;seconds\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_i\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Gravitional\mathit\;accelerational\mathit=\mathit\;g\mathit=\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Height\mathit\;\mathit=\mathit\;h\mathit\;\mathit=\mathit\;\mathit?\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_f\mathit\;\mathit=\mathit\;\mathit?\\\\\\Formula\mathit:\mathit-\\h\mathit\;\mathit=\mathit\;v_i\mathit\;t\mathit\;\mathit+\mathit\;\frac{\mathit1}{\mathit2}\mathit\;g\mathit\;t^{\mathit2}\\\\h=(0\;m\;s^{-1})\;(5\;s)+\frac12(10\;m\;s^{-2})\;{(5\;s)}^2\\\\h\;=\;0\;m\;+\;125\;m\\\\h\;=\;125\;m\\\\\\Formula:-\\v_{\mathrm f}\;=\;v_{\mathrm i}\;+\;g\;t\\\\\\v_f\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit+\mathit\;\mathit(\mathit\;\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;\mathit(\mathit\;\mathit5\mathit\;s\mathit\;\mathit)\\\\v_f\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit+\mathit\;\mathit{50}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\v_f\mathit\;\mathit=\mathit\;\mathit{50}\mathit\;m\mathit\;s^{\mathit-\mathit1}$$

====================================================================================

Smart Syllabus 9th class physics Chapter 3 Numerical

 

$$\boldsymbol3\boldsymbol{\mathit.}\boldsymbol1\;\;\;A\;10\;kg\;block\;is\;placed\\on\;a\;smooth\;horiznotal\\surface.\;A\;horizontal\;force\\of\;5N\;is\;applied\;to\;the\;block.\\Find:\\(a)\;the\;acceleration\;produced\\in\;the\;block.\\(b)\;the\;velocity\;of\;block\;after\\5\;seconds.$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Mass\;=\;m\;=\;10\;kg\\Force\;=\;F\;=\;5\;N\\Time\;=\;t\;=\;5\;s\\Initial\;velocity\;=\;v_i\;=\;0\\Acceleration\;=\;a\;=\;?\\Final\;velocity\;=\;v_f\;=\;?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol F\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol m\boldsymbol\;\boldsymbol a\\\\5\;N\;=\;(\;10\;kg\;)\;a\\\frac{5\;N}{10\;kg}\;=\;a\\\frac{1\;kg\;m\;s^{-2}}{2\;kg}=\;a\\a\;=\;0.5\;m\;s^{-2}\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\{\boldsymbol v}_{\mathbf f}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf i}\boldsymbol\;\boldsymbol+\boldsymbol\;\boldsymbol a\boldsymbol\;\boldsymbol t\\\\v_f\;=\;0\;+\;(\;0.5\;m\;s^{-2}\;)\;(\;5\;s\;)\\v_f\;=\;2.5\;m\;s^{-2}\;\\$$

========================================

$$\boldsymbol3\boldsymbol{\mathit.}\boldsymbol2\;\;\;\;The\;mass\;of\;person\;is\\80\;kg\;what\;will\;be\;his\;weight\\on\;the\;earth\;?\;what\;will\;be\;his\\weight\;on\;the\;moon.\;The\\value\;of\;acceleration\;due\;to\\gravity\;of\;moon\;is\;1.6\;m\;s^{-2}.$$

$$Data:-\\Mass\;=\;m\;=\;80\;kg\\Weight\;on\;Earth\;=\;w_e\;=\;?\\Acceleration\;on\;Earth=g=10\;m\;s^{-2}\\Acceleration\;on\;Moon=g_m=1.6\;m\;s^{-2}\\Weight\;on\;Moon\;=\;w_m\;=\;?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol F\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol w\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol m\boldsymbol\;\boldsymbol g\\\\w_e\;=\;m\;g\\w_e\;=\;(\;80\;kg\;)\;(\;10\;m\;s^{-2}\;)\;\\{\boldsymbol w}_{\mathbf e}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{800}\boldsymbol\;\boldsymbol N\\\\w_m\;=\;m\;g_m\\w_m\;=\;(\;80\;kg\;)\;(\;1.6\;m\;s^{-2}\;)\;\\{\boldsymbol w}_{\mathbf m}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{128}\boldsymbol\;\boldsymbol N$$

========================================

$$\boldsymbol3\boldsymbol{\mathit.}\boldsymbol3\;\;\;\;\;What\;force\;is\;required\\to\;increase\;the\;velocity\boldsymbol\;of\\800\;kg\;\;car\;from\;\;10\;m\;s^{-1}\\to\;\;30\;m\;s^{-1}\;\;in\;\;10\;seconds.$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;=\;m\;=\;800\;kg\\Initial\;velocity\;=\;v_i\;=\;10\;m\;s^{-1}\\Final\;velocity\;=\;v_f\;=\;30\;m\;s^{-1}\\Time\;=\;t\;=\;10\;s\\Force\;=\;F\;=\;?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol v}_{\boldsymbol f}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol v}_{\boldsymbol i}\boldsymbol{\mathit\;}\boldsymbol{\mathit+}\boldsymbol{\mathit\;}\boldsymbol a\boldsymbol{\mathit\;}\boldsymbol t\\\\v_f\;-\;v_i\;=\;a\;t\;\\\\\frac{v_f\;-\;v_i}t\;=\;a\\\\a\;=\frac{v_f\;-\;v_i}t\\\\a\;=\;\frac{30\;m\;s^{-1}\;-\;10\;m\;s^{-1}}{10\;s}\\a\;=\;\frac{20\;m\;s^{-1}}{10\;s}\\\\a\;=\;2\;m\;s^{-2}\;\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol F\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol{\mathit\;}\boldsymbol a\\\\F\;=\;(\;800\;kg\;)\;(\;2\;m\;s^{-2}\;)\\\\\boldsymbol F\boldsymbol=\boldsymbol\;\mathbf{1600}\boldsymbol\;\boldsymbol N\\$$

========================================

$$\boldsymbol3\boldsymbol{\mathit.}\boldsymbol4\;\;\;A\;5\;g\;bullet\;is\;fired\;from\\a\;gun.\;The\;bullet\;moves\;with\\a\;velocity\;of\;300\;m\;s^{-1}.\;\;If\\the\;mass\;of\;gun\;is\;\;10\;kg,\\find\;recoil\;speed\;of\;the\;gun.\\$$

$$Here,\;momentum\;before\;the\\collision\;is\;zero\\\;So\\m_{\mathit1}\mathit\;u_{\mathit1}\mathit\;\mathit+\mathit\;m_{\mathit2}\mathit\;u_{\mathit2}\;=\;0\\\\m_1u_1\mathit+m_2u_2\mathit=m_1v_1\mathit+m_2v_2\\\\0=(5\;g)\;(300\;ms^{-1})+(10\;kg)v_2\;\\\\0=(0.005\;kg)\;(300\;ms^{-1})+(10\;kg)v_2\\\\0\;=\;1.5\;kg\;m\;s^{-1}\;+\;(\;10\;kg\;)\;v_2\\\\-1.5\;kg\;m\;s^{-1}\;=\;(\;10\;kg\;)\;v_2\\\\\frac{-1.5\;kg\;m\;s^{-1}}{10\;kg}=\;v_2\\\\v_2\;=-\;0.15\;m\;s^{-1}\\\\Negative\;\mathrm{si}gn\;appears\;due\;to\\the\;recoil\;speed\;of\;gun.\\$$

=======================================

$$\boldsymbol3\boldsymbol{\mathit.}\boldsymbol7\;\;\;\;\;A\;cyclist\;weighing\\55\;kg\;rides\;a\;bicycle\;of\\mass\;5\;kg.\;He\;starts\;from\\rest\;and\;applies\;a\;force\;of\\90\;N\;for\;8\;seconds.\;Then\\he\;continues\;at\;a\;cons\tan t\\speed\;for\;another\;8\;seconds.\\Calculate\;the\;total\;dis\tan ce\\travelled\;by\;the\;cyclist.$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Total\;mass\;=m=55kg\;+\;5kg=\;60\;kg\\\\Initial\;velocity\;=\;v_i\;=\;0\\\\Force\;=\;F\;=\;90\;N\\\\Initial\;time\;=\;t_1\;=\;8\;seconds\\\\Further\;time\;=\;t_2\;=\;8\;seconds\\\\Total\;dis\tan ce\;=\;S\;=\;?\\\\$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol F\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol m\boldsymbol\;\boldsymbol a\;\\\\\frac Fm\;=\;a\\\\\frac{90\;N}{60\;kg}\;=\;a\\\\a\;=\;1.5\;m\;s^{-2}\\\\$$

$$Initial\;dis\tan ce\;=\;S_1\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol S\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf i}\boldsymbol\;\boldsymbol t\boldsymbol\;\boldsymbol+\boldsymbol\;\frac{\mathbf1}{\mathbf2}\boldsymbol\;\boldsymbol a\boldsymbol\;\boldsymbol t^{\mathbf2}\;\\\\S_1\;=\;0\;+\;(0.5)\;(\;1.5\;m\;s^{-2})\;{(8s)}^2\\\\S_1\;=\;48\;m\\\\\\$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\{\boldsymbol v}_{\mathbf f}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf i}\boldsymbol\;\boldsymbol+\boldsymbol\;\boldsymbol a\boldsymbol\;\boldsymbol t\boldsymbol\;\\\\v_f\;=\;0\;+\;(\;1.5\;m\;s^{-2}\;)\;{(\;8\;s\;)}\\\\v_f\;=\;12\;m\;s^{-1}\\\\\\\\\\$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol S\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf a\mathbf v}\boldsymbol\;\boldsymbol t\\\\Here\;t\;=\;t_{2\;}\;and\;\;v_{av}\;=\;v_f\;\;\\s_2\;=\;s\;(\;say\;)\\So\\\\S_2\;=\;(\;12\;m\;s^{-1}\;)\;(\;8\;s\;)\\\\S_2\;=\;96\;m\\\\\\\\\\\\$$

$$S\;=\;S_1\;+\;S_2\;\\\\S\;=\;48\;m\;+\;96\;m\\\\S\;=\;144\;m\\\\\\\\\\\\$$

====================================================================

Smart Syllabus 9th class physics Chapter 4 Numerical

$$4.1\boldsymbol{\mathit\;}\;\;A\;force\;of\;200\;N\;is\\acting\;on\;a\;cart\;at\;an\\angle\;of\;30\;degree\;with\\the\;horizontal\;direction.\\Find\;x\;and\;y\;components\\of\;the\;force\\\\\\\\$$

$$Data:-\\Force\;=\;F\;=\;200\;N\\Angle\;=\;\theta\;=\;30\;degree\\Horizontal\;component\;=\;F_x\;=\;?\\Vertical\;\;component\;=\;F_y\;=\;?\\$$

$$\\Formula:-\\F_{\mathrm x}\;=\;F\;cos\;\theta\\\\\\F_x\mathit\;\mathit=\mathit\;\mathit(\mathit{200}\mathit\;N\mathit)\mathit\;cos\mathit\;\mathit{30}\\\\F_x\mathit\;\mathit=\mathit\;\mathit(\mathit{200}\mathit\;N\mathit)\mathit\;\mathit\times\mathit\;\frac{\sqrt{\mathit3}}{\mathit2}\mathit\;\\\\F_x\mathit\;\mathit=\mathit\;\mathit(\mathit{100}\mathit\;N\mathit)\mathit\;\mathit\times\mathit\;\sqrt{\mathit3}\mathit\;\\\\F_x\mathit\;\mathit=\mathit\;\mathit(\mathit{100}\mathit\;N\mathit)\mathit\times\mathit1\mathit.\mathit{732}\\\\F_x\mathit\;\mathit=\mathit\;\mathit{173}\mathit.\mathit2\mathit\;N\\\\\\Formula:-\\F_{\mathrm y}\;=\;F\;sin\;\theta\\\\\\F_y\mathit\;\mathit=\mathit\;\mathit(\mathit{200}\mathit\;N\mathit)\mathit\;sin\mathit\;\mathit{30}\\\\F_y\mathit\;\mathit=\mathit\;\mathit(\mathit{200}\mathit\;N\mathit)\mathit\;\mathit\times\mathit\;\frac{\mathit1}{\mathit2}\mathit\;\\\\F_y\mathit\;\mathit=\mathit\;\mathit{100}\mathit\;N$$

====================================================================================

$$4.3\;\;\;\;\;\;\;Two\;weights\;are\\hanging\;from\;a\;meter\;rule\\at\;the\;positions\;as\;shown\\in\;the\;figure.\;If\;the\;meter\\rule\;is\;balanced\;at\;its\\centre\;of\;gravity\;(C.G),\;find\\the\;unknown\;weight\;w.$$

 

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\w_1\;=\;4\;N\\\\d_1\;=30\;cm\;=\;\frac{30}{100}m\;=\;0.3\;m\\\\d_2\;=40\;cm\;=\;\frac{40}{100}m\;=\;0.4\;m\\\\w\;=\;?\\$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol w}_{\boldsymbol1}\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}{\boldsymbol d}_{\boldsymbol1}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol w\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}{\boldsymbol d}_{\boldsymbol2}\;\\\\4\;N\;\times\;0.3\;m\;=\;w\;\times\;0.4\;m\\\\w\;=\;\frac{4\;N\;\times\;0.3\;m}{0.4\;m}\\\\w\;=\;3\;N\\\\\\$$

====================================================================================

$$4.4\;\;\;A\;sea-saw\;is\;balanced\\with\;two\;children\;sitting\;near\\either\;end.\;Child\;A\;weighs\\30\;kg\;and\;sits\;2\;metres\;away\\from\;the\;pivot,\;while\;child\;B\\weighs\;40\;kg\;and\;sits\;1.5\\metres\;from\;the\;piovt.\\Calculate\;the\;total\;moment\\on\;each\;side\;and\;determine\\if\;sea-saw\;is\;in\;eqilibrium.$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;of\;chlid\;A\;=\;m_1\;=\;30\;kg\\\\Mass\;of\;chlid\;B\;=\;m_1\;=\;40\;kg\\\\Dis\tan ce\;of\;child\;A\;from\;pivot\;\\=l_1\;=\;2\;m\\\\Dis\tan ce\;of\;child\;B\;from\;pivot\;\\=l_2\;=\;1.5\;m\\\\Moment\;of\;child\;A\;=\;\tau_1\;=\;?\\\\Moment\;of\;child\;A\;=\;\tau_2\;=\;?\\$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\\boldsymbol T\boldsymbol o\boldsymbol r\boldsymbol q\boldsymbol u\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol\tau\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol F\\\boldsymbol T\boldsymbol o\boldsymbol r\boldsymbol q\boldsymbol u\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol\tau\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol W\\\boldsymbol T\boldsymbol o\boldsymbol r\boldsymbol q\boldsymbol u\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol\tau\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol g\\\\Moment\;of\;child\;A={\boldsymbol\tau}_{\mathbf1}=l_1\times F_1\\\\=l_1\times w_1=l_1\times m_1g\\=(2\;m)\times(30\;kg)(10\;m\;s^{-2})\\\\=\;(2\;m)\;(300\;kgms^{-2})\\=600\;Nm\\\\\\Moment\;of\;child\;B={\boldsymbol\tau}_{\mathbf2}=l_2\times F_2\\\\=\;l_2\times w_2=l_2\;\times\;m_2\;g\\=(1.5m)\times(40\;kg)(10\;m\;s^{-2})\\\\=\;(1.5\;m)\times(400\;kg\;m\;s^{-2})\;\\=\;600\;Nm\\\\\\\;Since\;\boldsymbol{\mathit\;}{\boldsymbol\tau}_{\boldsymbol1\boldsymbol{\mathit\;}}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol\tau}_{\boldsymbol2\boldsymbol{\mathit\;}}\\Therefore\;system\;is\\in\;equilibrium.\\$$

====================================================================================

$$4.7\;\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}A\;5\;N\;ball\;hanging\\from\;a\;rope\;is\;pulled\;to\\the\;right\;by\;a\;horizontal\\force\;F.\;This\;rope\;makes\\an\;angle\;of\;60^\circ\;with\;the\\ceiling,\;as\;shown\;in\;the\\given\;figure.\;Determine\\the\;magnitude\;of\;force\;F\\and\;tension\;T\;in\;the\;string.\\\\\\\\$$

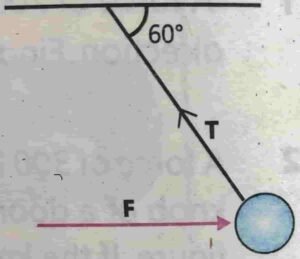
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\\\Weight\;of\;ball\;=\boldsymbol\;\boldsymbol w\;=?\;\\\\Angle\;=\;\theta\;=\;60\;degree\\\\Force\;=\;\boldsymbol F\;=?\\\\Tension\;=\;T\;=?\\\\\\\\\\$$

$$\boldsymbol F\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol w\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf5\boldsymbol\;\boldsymbol N\\\\\boldsymbol V\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol i\boldsymbol c\boldsymbol a\boldsymbol l\boldsymbol l\boldsymbol y\\\\T_y\;=\;w\\\\\boldsymbol T\boldsymbol\;\boldsymbol s\boldsymbol i\boldsymbol n\boldsymbol\;\boldsymbol\theta\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol w\\\\\boldsymbol T\;\sin\;60\;=\;5\;N\\\\\boldsymbol T\;(\frac{\sqrt3}2)\;=\;5\;N\\\\\boldsymbol T\;=\;\frac{5\;N}{\frac{\sqrt3}2}\\\\\boldsymbol T\;=\;\frac{10}{\sqrt3}N\\\\\boldsymbol T\boldsymbol\;=\;5.77\;N\\\\\\\boldsymbol H\boldsymbol o\boldsymbol r\boldsymbol i\boldsymbol z\boldsymbol o\boldsymbol n\boldsymbol t\boldsymbol a\boldsymbol l\boldsymbol l\boldsymbol y\boldsymbol\;\\\\\\\boldsymbol F\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol T\boldsymbol\;\boldsymbol c\boldsymbol o\boldsymbol s\boldsymbol\;\boldsymbol\theta\\\\\boldsymbol F\;=\;5.77\;N\;\times\;0.5\;\\\\\boldsymbol F\;=\;2.89\;N\\\\\\\\\\\\$$

====================================================================================

$$4.8\;\;\;A\;sign\;board\;is\\suspended\;by\;mans\\of\;two\;steel\;wires\;as\\shown\;in\;the\;given\;figure.\\If\;the\;weight\;of\;the\;board\\is\;200\;N,\;what\;is\;the\\tension\;in\;the\;strings\;?$$

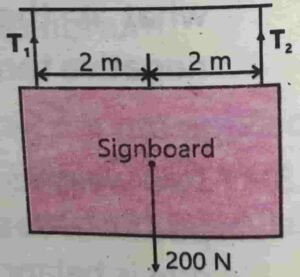
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\weight\;=\;w\;=\;200\;N\\\\Tension\;is\;1st\;string\;=\;T_1\;=\;?\\\\Tension\;is\;2nd\;string\;=\;T_2\;=\;?$$

$$Vertical\;forces\;will\;balance\;each\;other\\\\{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol+\boldsymbol\;{\boldsymbol T}_{\mathbf2}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{200}\boldsymbol\;\boldsymbol N\\\\Wires\;are\;symmetrically\;placed.\\\\Hence\;\\\\{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol T}_{\mathbf2}\boldsymbol\;\\\\So\\{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol+\boldsymbol\;{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{200}\boldsymbol\;\boldsymbol N\\\\2{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol\;=\;200\;N\\\\{\boldsymbol T}_{\mathbf1}\;=\;\frac{\;200\;N}2\\\\{\boldsymbol T}_{\mathbf1}\;=\;100\;N\\\\But\\{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol T}_{\mathbf2}\\\\So\;\\\\{\boldsymbol T}_{\mathbf2}\;=\;100\;N\\\\\\\\$$

$$Hence\;tension\;in\;each\;string\;in\;\boldsymbol{100}\boldsymbol{\mathit\;}\boldsymbol N\\\\\\\\$$

====================================================================================

Smart Syllabus 9th class physics Chapter 5 Numerical

$$\mathit5\mathit.\mathit1\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}A\;force\;of\;20\;N\;acting\\at\;an\;angle\;of\;60\;degree\\to\;the\;horizontal\;is\;used\\to\;pull\;a\;box\;through\;a\\dis\tan ce\;of\;3\;m\;across\\a\;floor.\;How\;much\\work\;is\;done\;?\\\\$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Force\;=\boldsymbol\;\boldsymbol F\;=\;20\;N\\\\Angle\;=\;\theta\;=\;60\;degree\\\\Dis\tan ce\;=\boldsymbol\;\boldsymbol S\;=\;3\;m\\\\Work\;=\;W\;=\;?\\\\$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol W\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol F\boldsymbol S\boldsymbol{\mathit\:}\boldsymbol c\boldsymbol o\boldsymbol s\boldsymbol{\mathit\;}\boldsymbol\theta\\\\$$

$$W\;=\;(\;20\;N\;)\;(\;3\;m\;)\;\cos\;60\\\\W\;=\;(\;60\;Nm\;)\;(\;0.5\;)\\\\W\;=\;30\;J\\\\$$

====================================================================================

$$\mathit5\mathit.\mathit3\;\;\;\;\;An\;engine\;raises\\100\;kg\;of\;water\;through\\a\;height\;of\boldsymbol\;80\;m\;\;in\;25s.\\what\;is\;the\boldsymbol\;power\;of\\the\;engine\;?$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;of\;water\;=\;m\;=\;100\;kg\\\\Height\;=\;h\;=\;80\;m\\\\time\;=\;t\;=\;25\;s\\\\power\;=\;\boldsymbol P\boldsymbol\;=\;?$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\\boldsymbol p\boldsymbol o\boldsymbol w\boldsymbol e\boldsymbol r\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol w\boldsymbol o\boldsymbol r\boldsymbol k}{\boldsymbol t\boldsymbol i\boldsymbol m\boldsymbol e}\\\boldsymbol P\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol W}{\boldsymbol t}\\\boldsymbol P\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol m\boldsymbol g\boldsymbol h}{\boldsymbol t}\\\\P\;=\;\frac{(100\;kg)\;(10\;m\;s^{-2})\;(80\;m)}{25\;s}\\\\P\;=\;3200\;kg\;m^2\;s^{-2}\;s^{-1}\\\\P\;=\;3200\;kg\;m\;s^{-2}\;m\;\;s^{-1}\\\\P\;=\;3200\;N\;m\;s^{-1}\\\\P\;=\;3200\;J\;s^{-1}\\\\P\;=\;3200\;W\\\\$$

====================================================================================

$$\mathit5\mathit.\mathit4\;\;A\;body\;of\;mass\boldsymbol\;20\;kg\\\;is\;at\;rest.\;A\boldsymbol\;40\;N\boldsymbol\;force\\acts\;on\;it\;for\;5\;seconds.\\What\;is\;the\;kinetic\;energy\\of\;the\;body\;at\;the\;end\\of\;this\;time\;?\\\\\\$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Initial\;velocity\;=\boldsymbol\;{\boldsymbol v}_{\mathbf i}\boldsymbol\;=\;0\;m\;s^{-1}\\\\Mass\;=\;m\;=\;20\;kg\\\\Force\;=\;\boldsymbol F\;=\;40\;N\\\\Time\;=\;t\;=\;5\;s\\\\Kinetic\;energy\;=\boldsymbol\;\boldsymbol K\boldsymbol\;\boldsymbol.\boldsymbol\;\boldsymbol E\;=\;?\\\\\\$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol F\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol{\mathit\;}\boldsymbol a\\\\40\;\mathrm N\;=\;(\;20\;\mathrm{Kg}\;)\boldsymbol\;\mathbf a\\\\\frac{40\;\mathrm N}{20\;\mathrm{Kg}}\;=\boldsymbol\;\mathbf a\\\\\mathbf a\;=\;\frac{40\;\mathrm{kg}\;\mathrm m\;\mathrm s^{-2}}{20\;\mathrm{Kg}}\\\\\boldsymbol a\;=\;2\;m\;s^{-2}\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol v}_{\boldsymbol f}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol v}_{\boldsymbol i}\boldsymbol{\mathit\;}\boldsymbol{\mathit+}\boldsymbol{\mathit\;}\boldsymbol a\boldsymbol{\mathit\;}\boldsymbol t\boldsymbol{\mathit\;}\\\\{\boldsymbol v}_{\mathbf f}\;=\;0\;+\;(\;\;2\;m\;s^{-2}\;)\;(\;5\;s\;)\;\\\\{\boldsymbol v}_{\mathbf f}\;=\;10\;m\;s^{-1}\\$$

$$Here\\{\boldsymbol v}_{\mathbf f}\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol v\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol K\boldsymbol{\mathit.}\boldsymbol E\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol1}{\boldsymbol2}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol{\mathit\;}\boldsymbol v^{\boldsymbol2}\\\\K.\;E\;=\;\frac12\;(\;20\;kg\;)\;{(\;10\;m\;s^{-1}\;)}^2\\\\K.\;E\;=\;\;(\;10\;kg\;)\;(\;10\;m^2\;s^{-2}\;)\\\\K.\;E\;=\;100\;kg\;m\;s^{-2}\;m\\\\K.\;E\;=\;100\;N\;m\\\\\boldsymbol K\boldsymbol.\boldsymbol E\;=\;100\;J\\$$

====================================================================================

$$\mathit5\mathit.\mathit6\;\;\;\;A\;0.14\;kg\;ball\;is\\thrown\;vertically\;upward\\with\;an\;initial\;velocity\;of\\35\;m\;s^{-1}.\;Find\;maximum\\height\;reached\;by\;the\;ball.\\\\\\\\$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;=\;m\;=\;0.14\;kg\\\\Initial\;velocity\;=\boldsymbol\;{\boldsymbol v}_{\mathbf i}\;=\;35\;m\;s^{-1}\\\\Final\;velocity\;=\boldsymbol\;{\boldsymbol v}_f\;=\;0\;m\;s^{-1}\\\\Gravitional\;acceleration\;=\;\boldsymbol g\;=\;10\;m\;s^{-2}\\\\Height\;=\;h\;=\;?\\\\\\\\\\$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol K\boldsymbol{\mathit.}\boldsymbol E\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol1}{\boldsymbol2}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol{\mathit\;}\boldsymbol v^{\boldsymbol2}\\Here\;\\\\v_i\;=\;v\\\\So\;\\\\\boldsymbol K\boldsymbol{\mathit.}\boldsymbol E\boldsymbol{\mathit\;}=\;\frac12(0.14\;kg)\;\;{(\;35\;m\;s^{-1})}^2\\\\K.E\;=\;85.75\;J\\\\\\\\\\\\\\\\$$

$$At\;the\;maximun\;height\\kinetic\;energy\;is\;toally\\converted\;into\\potential\;energy\\\\Hence\\\\potential\;energ\boldsymbol y\;=\;85.75\;Joules\\$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol P\boldsymbol{\mathit.}\boldsymbol E\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol{\mathit\;}\boldsymbol g\boldsymbol{\mathit\;}\boldsymbol h\\\\85.75\;J\;=\;(\;0.14\;kg\;)\;(\;10\;m\;s^{-2}\;)\;h\\\\\frac{85.75\;J}{\;(\;0.14\;kg\;)\;(\;10\;m\;s^{-2}\;)\;}\;=\;h\\\\h\;=\;\frac{85.75\;N\;m}{1.4\;kg\;m\;s^{-2}}\\\\h\;=\;\;\frac{85.75\;N\;m}{1.4\;N}\\\\h\;=\;61.25\;m\\\\\\\\\\\\\\\\\\$$

====================================================================================

 

$$5.10\boldsymbol\;\boldsymbol\;\boldsymbol\;\boldsymbol\;\boldsymbol\;\boldsymbol\;\boldsymbol\;\boldsymbol\;\boldsymbol\;\boldsymbol\;A\;box\;of\;mass\\10\;kg\;is\;pushed\;up\;along\\a\;ramp\;15\;m\;long\;with\;a\\force\;of\;80\;N.\;If\;the\;box\\rises\;up\;a\;height\;of\;5\;m,\\what\;is\;the\;efficiency\\of\;the\;system\;?\\\\$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;of\;box\;=\;m\;=\;10\;kg\\\\Dis\tan ce\;=\;S\;=\;15\;m\\\\Height\;=\;h\;=\;5\;m\\\\Force\;=\;F\;=\;80\;N\\\\Gravitional\;acceleration\;=\;g\;=\;9.8\;m\;s^{-2}\\\\\boldsymbol E\boldsymbol f\boldsymbol f\boldsymbol i\boldsymbol c\boldsymbol i\boldsymbol e\boldsymbol n\boldsymbol c\boldsymbol y\;=\;?\\$$

$$Work\mathit\;done\mathit\;is\mathit\;input\mathit\;and\\Energy\;gained\mathit\;is\mathit\;output.\\$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol W\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol F\boldsymbol{\mathit\;}\boldsymbol S\\\\W\;=\;(\;80\;N\;)\;(\;15\;m\;)\\\\W\;=\;1200\;J\\\\So\\Input\;=\;1200\;J\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol P\boldsymbol o\boldsymbol t\boldsymbol n\boldsymbol e\boldsymbol t\boldsymbol i\boldsymbol a\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol e\boldsymbol n\boldsymbol e\boldsymbol r\boldsymbol g\boldsymbol y\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol{\mathit\;}\boldsymbol g\boldsymbol{\mathit\;}\boldsymbol h\boldsymbol{\mathit\;}\\\\P.\;E\;=\;(\;10\;kg\;)\;(\;10\;m\;s^{-2}\;)\;(\;5\;m\;)\\\\P.\;E\;=\;500\;J\\\\So\\Output\;=\;500\;J\\$$ $$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol E\boldsymbol f\boldsymbol f\boldsymbol i\boldsymbol c\boldsymbol i\boldsymbol e\boldsymbol n\boldsymbol c\boldsymbol y\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol o\boldsymbol u\boldsymbol t\boldsymbol p\boldsymbol u\boldsymbol t}{\boldsymbol i\boldsymbol n\boldsymbol p\boldsymbol u\boldsymbol t}\\\\Efficency\;\%\;=\;(\frac{output}{input}\;)\;100\;\%\\\\Efficency\;\%\;=\;(\frac{500}{1200}\;)\;100\;\%\\\\Efficency\;\%\;=\;(\;0.417\;)\;100\;\%\\\\\boldsymbol E\boldsymbol f\boldsymbol f\boldsymbol i\boldsymbol c\boldsymbol e\boldsymbol n\boldsymbol c\boldsymbol y\boldsymbol\;\boldsymbol\%\;=\;41.7\;\%$$

====================================================================================

$$\mathit5\mathit.\mathit{11}\;\;\;\;\;\;\;A\;force\;of\\600\;N\;acts\;on\;a\;box\;to\\push\;it\;\;5\;m\;\;in\;\boldsymbol\;15\;s.\\Calculate\;the\;power.$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Force\;=\boldsymbol\;\boldsymbol F\;=\;600\;N\\\\Dis\tan ce\;=\;S\;=\;5\;m\\\\Time\;=\;t\;=\;15\;s\\\\Power\;=\;P\;=\;?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol P\boldsymbol o\boldsymbol w\boldsymbol e\boldsymbol r\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol w\boldsymbol o\boldsymbol r\boldsymbol k}{\boldsymbol T\boldsymbol i\boldsymbol m\boldsymbol e}\\\boldsymbol P\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol W}{\boldsymbol t}\\\\P\;=\;\frac{F\;S}t\\\\P\;=\;\frac{(\;600\;N\;)\;(\;5\;m\;)}{15\;s}\\\\P\;=\;\frac{(\;3000\;N\;m\;)}{15\;s}\\\\P\;=\;200\;J\;s^{-1}\\\\P\;=\;200\boldsymbol\;\boldsymbol w\boldsymbol a\boldsymbol t\boldsymbol t\\\\$$

====================================================================================

Smart Syllabus 9th class physics Chapter 6 Numerical

 

$$6.1\;\;A\;spring\;is\;stretched\\20\;mm\;by\;a\;load\;of\;40\;N.\\Calculate\;the\;value\;of\\spring\;constant.\;If\;an\\object\;causes\;an\\extension\;of\;16\;mm,\\what\;will\;be\;its\;weight\;?\\$$

$$\mathrm{Data}:-\\Dis\tan ce\;=\;x\;=\;20\;mm\\=\;\frac{20}{1000}\;m\;=\;0.02\;m\\Force\;=\;F\;=\;40\;N\\Spring\;cons\tan t\;=\;k\;=\;?\\\\Extension\;=\;x_1\;=16\;mm\\=\frac{16}{1000}m=\;0.016\;m\\Weight\;=\;w\;=\;?$$

$$F\mathit\;\mathit=\mathit\;k\mathit\;x\\k\;=\;\frac Fx\\\\k\;=\;\frac{40\;N}{0.02\;m}\\k\;=\;2000\;N\;m^{-1}\\k\;=\;2\;K\;N\;m^{-1}$$ $$w\mathit\;\mathit=\mathit\;F\mathit\;\mathit=\mathit\;k\mathit\;x\\w\;=\;(\;2000\;N\;m^{-1}\;)\;(\;0.016\;m\;)\\w\;=\;32\;N\\$$

==========================================

$$\mathit6\mathit.\mathit2\;\;The\;mass\;of\;5\\litres\;milk\;is\;4.5\;kg.\\Find\;its\;density\;in\\SI\;units.\\\\$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;=\;m\;=\;4.5\;kg\\\\Volume\;=\;V\;=\;5\;litre\;\\=\;\frac5{1000}\;m^3\;=\;0.005\;m^3\;\\\\Density\;=\;\rho\;=\;?\\$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol D\boldsymbol e\boldsymbol n\boldsymbol s\boldsymbol i\boldsymbol t\boldsymbol y\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol m\boldsymbol a\boldsymbol s\boldsymbol s}{\boldsymbol v\boldsymbol o\boldsymbol l\boldsymbol u\boldsymbol m\boldsymbol e}\boldsymbol{\mathit\;}\\\\\boldsymbol\rho\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol m}{\boldsymbol V}\\$$

$$\rho\;=\;\frac{4.5\;kg}{0.005\;m^3}\\\\\rho\;=\;900\;kg\;m^{-3}\\\\\rho\;=\;0.9\;\times\;10^3\;kg\;m^{-3}\\$$

==========================================

$$\mathit6\mathit.\mathit4\;\;\;\;A\;block\;of\;density\mathit\;\\\mathit8\mathit\;\mathit\times\mathit\;\mathit{10}^{\mathit3}\mathit\;kg\mathit\;m^{\mathit-\mathit3}\;has\;a\\volume\mathit\;\mathit\;\mathit{60}\mathit\;c\mathit\;m^{\mathit3}.\;\;Find\\its\;mass.\\$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Density\;=\;\rho\;=\;8\;\times\;10^3\;kg\;m^{-3}\\\\Volume\;=\;V\;=\;60\;c\;m^3\;=\\\\=\;\frac{60}{1000000}\;m^3\;=\;0.00006\;m^3\\\\Mass\;=\;m\;=\;?\\$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol D\boldsymbol e\boldsymbol n\boldsymbol s\boldsymbol i\boldsymbol t\boldsymbol y\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol m\boldsymbol a\boldsymbol s\boldsymbol s}{\boldsymbol v\boldsymbol o\boldsymbol l\boldsymbol u\boldsymbol m\boldsymbol e}\boldsymbol{\mathit\;}\\\boldsymbol\rho\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol m}{\boldsymbol V}\\$$

$$m\mathit\;\mathit=\mathit\;\rho\mathit\;V\\\\m\;=\;(\;8\;\times\;10^3\;kg\;m^{-3}\;)\;\;(\;0.00006\;m^3\;)\\\\m\;=\;0.48\;kg\\$$

==========================================

$$\mathit6\mathit.\mathit5\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}A\;brick\;measures\\5\;cm\;\times\;10\;cm\;\times20\;cm.\\If\;its\;mass\;is\;5\;kg,\\calculate\;the\;\;maximum\\and\;minimum\;pressure\;\\which\;the\;brick\;can\\exert\;on\;a\;horizontal\\surface.$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Mass\;=\;m\;=\;5\;kg\\\\Masurement\;of\;brick\;=B\\=\;5cm\;\times10cm\times20cm\\\\5cm\;=\;\frac5{100}\;m\;=\;0.05\;m\\\\10cm\;=\;\frac{10}{100}\;m\;=\;0.10\;m\\\\20cm\;=\;\frac{20}{100}\;m\;=\;0.20\;m\\\\Hence\\\\Measurement\;of\;brick=B\\=0.05m\times0.1m\times0.2m\\\\Maximum\;pressure\;=\;P_1\;=\;?\\\\Minimum\;Pressure\;=\;P_2\;=\;?\\$$

$$\boldsymbol S\boldsymbol o\boldsymbol l\boldsymbol u\boldsymbol t\boldsymbol i\boldsymbol o\boldsymbol n\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Area\;of\;face\;\boldsymbol A\;=\;0.05m\;\times\;0.1m\;\\=\;0.005\;m^2\\\\Area\;of\;face\boldsymbol\;\boldsymbol B\;=\;0.2m\;\times\;0.1m\;\\=\;0.02\;m^2\\\\Area\;of\;face\;\boldsymbol C\;=\;0.05m\;\times\;0.2m\;\\=\;0.01\;m^2\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol P\boldsymbol\;\boldsymbol=\boldsymbol\;\frac{\mathbf F}{\mathbf A}\\\\Here\;\boldsymbol F\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol w\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol{\mathit\;}\boldsymbol g\\\\F\;=\;w=\;(5\;k\;g)\;(10\;m\;s^{-2})\\\\\boldsymbol F\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol{50}\boldsymbol{\mathit\;}\boldsymbol N\\\\So\\\boldsymbol P\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol{50}\boldsymbol{\mathit\;}\boldsymbol N}{\boldsymbol A\boldsymbol r\boldsymbol e\boldsymbol a}\\\\Pressure\;of\;Face\boldsymbol\;\boldsymbol A\boldsymbol\;=\;\frac{50\;N}{0.005\;m^2}\;\\\\=\;10000\;N\;m^{-2}\;=\;10^4\;Pa\;\\\\Pressure\;of\;Face\boldsymbol\;\boldsymbol B\boldsymbol\;=\;\frac{50\;N}{0.02\;m^2}\;\\\\=\;2500\;N\;m^{-2}\;=\;25\;\times\;10^2\;Pa\\\\Pressure\;of\;Face\boldsymbol\;\boldsymbol C\boldsymbol\;=\;\frac{50\;N}{0.01\;m^2}\\\;\\=\;5000\;N\;m^{-2}\;=\;50\;\times\;10^2\;Pa\\\\Hence\\\\\boldsymbol M\boldsymbol a\boldsymbol x\boldsymbol i\boldsymbol m\boldsymbol u\boldsymbol m\boldsymbol{\mathit\;}\boldsymbol p\boldsymbol r\boldsymbol e\boldsymbol s\boldsymbol s\boldsymbol u\boldsymbol r\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol i\boldsymbol s\boldsymbol{\mathit\;}\boldsymbol o\boldsymbol n\boldsymbol{\mathit\;}\boldsymbol F\boldsymbol a\boldsymbol c\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol A\boldsymbol{\mathit\;}\\\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{10}^{\boldsymbol4}\boldsymbol{\mathit\;}\boldsymbol P\boldsymbol a\boldsymbol{\mathit\;}\\\boldsymbol M\boldsymbol i\boldsymbol n\boldsymbol i\boldsymbol m\boldsymbol u\boldsymbol m\boldsymbol{\mathit\;}\boldsymbol p\boldsymbol r\boldsymbol e\boldsymbol s\boldsymbol s\boldsymbol u\boldsymbol r\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol i\boldsymbol s\boldsymbol{\mathit\;}\boldsymbol o\boldsymbol n\boldsymbol{\mathit\;}\boldsymbol F\boldsymbol a\boldsymbol c\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol B\boldsymbol{\mathit\;}\\\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol{25}\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol{10}^{\boldsymbol2}\boldsymbol{\mathit\;}\boldsymbol P\boldsymbol a\\$$

==========================================

$$\mathit6\mathit.\mathit6\;\;\;\;What\;will\;be\;the\;height\\of\;a\;column\;in\;a\;barometer\\at\;sea\;level\;if\;mercury\;is\\replaced\;by\;water\;of\;density\\1000\;kg\;m^{-3},\;where\;density\\of\;mercury\;is\;\\13.6\;\times\;10^3\;kg\;m^{-3}\\$$

$$Density\;of\;water\;=\;\rho_w\\\;=\;1000\;kg\;m^{-3}\\\\Density\;of\;mercury=\;\rho_m\\=13.6\times10^3\;kg\;m^{-3}\\\\Height\;of\;mercury\;at\;sea\;level=h_m\\=760mm\\\\=\;\frac{760}{1000}\;m\;=\;0.76\;m\\\\Height\;of\;water\;at\;sea\;level=h_w=?\\\\P\;=\;\rho\;g\;h\\\\So\\\rho_{\mathrm w}\;g\;h_{\mathrm w}\;=\;\rho_{\mathrm m}\;g\;h_{\mathrm m}\\\\\rho_w\;\;h_w\;\;=\;\rho_m\;\;h_m\\\;\\h_w\;=\;\frac{\rho_m\;\;h_m}{\rho_w}\\\\h_w\;=\;\frac{(13.6\times10^3\;kgm^{-3})\;(\;0.76\;m)}{1000\;kg\;m^{-3}}\\\\h_w\mathit\;\mathit=\mathit\;\mathit{10}\mathit.\mathit{336}\mathit\;m$$

==========================================

$$\mathit6\mathit.\mathit7\;\;\;\;Suppose\;in\;the\\hydraulic\;brake\;system\;of\\a\;car,\;the\;force\;exerted\\normally\;on\;its\;piston\\of\;cross-sectional\;area\;of\;\\5\;c\;m^2\;is\;\;500\;N.\;What\;will\\be\;the\;pressure\;transferred\\to\;the\;brake\;oil?\;What\;will\\be\;the\;force\;on\;the\;second\\piston\;of\;area\;of\\cross\;section\;\;20\;c\;m^2\\$$

$$Force\;of\;1st\;piston\;=\;F_1\;=\;500\;N\\Area\;of\;1st\;piston=A_1=5\;c\;m^2\\=5\;\times\;10^{-4}\;m^2\\Area\;of\;1st\;piston=A_2=20\;c\;m^2\\=20\;\times\;10^{-4}\;m^2\\Pressure\;transimitted\;to\\brake\;oil=P=?\\Force\;of\;2nd\;piston\;=\;F_2\;=\;?\\\\Pressure\mathit\;\mathit=\mathit\;\frac{Force}{Area}\\P\mathit\;\mathit=\mathit\;\frac{F_{\mathit1}}{A_{\mathit1}}\\P\;=\;\frac{500\;N}{5\;\times\;10^{-4}\;m^2}\\P\mathit\;\mathit=\mathit\;\mathit{10}^{\mathit6}\mathit\;N\mathit\;m^{\mathit-\mathit2}\;\\\\\\P\mathit\;\mathit=\mathit\;\frac{F_{\mathit2}}{A_{\mathit2}}\\F_2\;=\;P\;A_2\;\\F_2=(10^6\;Nm^{-2})\;(20\times10^{-4}m^2)\\\\F_{\mathit2}\mathit\;\mathit=\mathit\;\mathit{2000}\mathit\;N$$

==========================================

$$6.9\;\;\;\;\;\;\;The\;area\;of\\cross\;section\;of\;the\;small\\and\;large\;pistons\;of\;a\\hydraulic\;press\;is\;respectively\\10\;c\;m^2\;and\;100\;c\;m^2.\\What\;force\;should\;be\\exerted\;on\;the\;small\;piston\\in\;order\;to\;lift\;a\;car\;of\\weight\;\;4000\;N$$

$$Area\;of\;small\;piston=A_1=10\;c\;m^2\\\\=\;\frac{10}{10000}m\;=\;0.001\;m^2\\\\Area\;of\;large\;piston=A_2=100\;c\;m^2\\\\=\;\frac{100}{10000}m\;=\;0.01\;m^2\\\\Weight\;of\;car=w=F_2=4000\;N\\\\Force\;on\;small\;piston\;=\;F_1\;=\;?\\Pressure\mathit\;\mathit=\mathit\;\frac{Force}{Area}\\P\mathit\;\mathit=\mathit\;\frac FA\\So\\\\\frac{F_1}{A_1}\;=\;\frac{F_2}{A_2}\;\\\\F_1\;=\;\frac{F_2\;A_1\;}{A_2}\\\\F_1\;=\;\frac{(\;4000\;N\;)\;(\;0.001\;m^2\;)}{0.01\;m^2}\\\\F_1\;=\;400\;N$$

==========================================

Smart Syllabus 9th class physics Chapter 7 Numerical

$$\mathit7\mathit.\mathit1\;\;\;The\;temperature\;of\\normal\;human\;body\;on\\Fahrenheit\;scale\;is\;98.6\\degree.\;Convert\;it\;into\\Celsius\;scale\;and\\Kelvin\;scale\boldsymbol.$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Temperature\;on\;Fahrenheit\;=\;{\boldsymbol T}_{\mathbf F}\;=\;98.6\\Temperature\;on\;Celsius\;=\boldsymbol\;{\boldsymbol T}_{\mathbf c}\;=\;?\\Temperature\;on\;Kelvin\;=\;{\boldsymbol T}_{\mathbf k}\;=\;?\\$$$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\{\boldsymbol T}_{\mathbf c}\boldsymbol\;\boldsymbol=\boldsymbol\;\frac{\mathbf5}{\mathbf9}\boldsymbol\;\boldsymbol(\boldsymbol\;{\boldsymbol T}_{\mathbf F}\boldsymbol\;\boldsymbol-\boldsymbol\;\mathbf{32}\boldsymbol\;\boldsymbol)$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\{\boldsymbol T}_{\mathbf k}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol T}_{\mathbf c}\boldsymbol\;\boldsymbol+\boldsymbol\;\mathbf{273}\\$$

$$T_c\;=\;\frac59\;(\;T_F\;-\;32\;)\\T_c\;=\;\frac59\;(\;98.6\;-\;32\;)\\\\T_c\;=\;(\;0.5556\;)\;(\;66.6667\;)\\\\T_c\;=\;37.02\;\\\\{\boldsymbol T}_{\mathbf c}\boldsymbol\;\boldsymbol\approx\boldsymbol\;\mathbf{37}\boldsymbol\;\boldsymbol d\boldsymbol e\boldsymbol g\boldsymbol r\boldsymbol e\boldsymbol e\\\\T_k\;=\;T_F\;+\;273\\T_k\;=\;37\;+\;273\\{\boldsymbol T}_{\mathbf k}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{310}\boldsymbol\;\boldsymbol k\boldsymbol e\boldsymbol l\boldsymbol v\boldsymbol i\boldsymbol n\\$$

==========================================

$$\mathit7\mathit.\mathit2\;\;At\;what\;temperature\\Celsius\;and\;Fehrenheit\\thermometer\;reading\\would\;be\;the\;same\;?$$

$$\boldsymbol C\boldsymbol e\boldsymbol l\boldsymbol s\boldsymbol i\boldsymbol u\boldsymbol s\boldsymbol{\mathit\;}\boldsymbol r\boldsymbol e\boldsymbol a\boldsymbol d\boldsymbol i\boldsymbol n\boldsymbol g\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol F\boldsymbol a\boldsymbol h\boldsymbol r\boldsymbol e\boldsymbol n\boldsymbol h\boldsymbol e\boldsymbol i\boldsymbol t\boldsymbol{\mathit\;}\boldsymbol r\boldsymbol e\boldsymbol a\boldsymbol d\boldsymbol i\boldsymbol n\boldsymbol g\\{\boldsymbol T}_{\boldsymbol c}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}{\boldsymbol T}_{\boldsymbol f}\boldsymbol{\mathit\;}\\\\T_c\;=\;\frac95\;T_c\;+\;32\\\\5\;T_c\;=\;9\;T_c\;+\;160\\\\5\;T_c\;-\;9\;T_c\;=\;160\\\\-4\;T_c\;=\;160\\\\T_c\;=\;\frac{160}{-4}\\\\T_c\;=\;-\;40\\\\The\;temperature\;at\;which\;Celsius\\and\;Fahrenheit\;scales\;show\;the\\same\;reading\;is\;\;\boldsymbol-\mathbf{40}\boldsymbol\;\boldsymbol d\boldsymbol e\boldsymbol g\boldsymbol r\boldsymbol e\boldsymbol e$$

==========================================

$$7.3\;\;\;Convert\;5\;degree\\Fahrenheit\;to\;Celsius\\and\;\;Kelvin\;scale.$$

$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol T}_{\mathbf c}\boldsymbol\;\boldsymbol=\boldsymbol\;\frac{\mathbf5}{\mathbf9}\boldsymbol\;\boldsymbol({\boldsymbol T}_{\mathbf f}\boldsymbol\;\boldsymbol-\boldsymbol\;\mathbf{32}\boldsymbol)\\\\T_c\;=\;\frac59\;(5\;-\;32)\\\\T_c\;=\;\frac59(-\;27\;)\\\\T_c\;=\;5\;(\;-3\;)\\\\{\boldsymbol T}_{\mathbf c}\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol-\boldsymbol\;\mathbf{15}\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol T}_{\mathbf k}\boldsymbol\;\boldsymbol={\boldsymbol T}_{\mathbf c}\boldsymbol\;\boldsymbol+\boldsymbol\;\mathbf{273}\\\\T_k\;=\;-15\;+\;273\\\\{\boldsymbol T}_{\mathbf k}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{258}$$

==========================================

$$7.4\;\;\;\;What\;is\;equivalent\\temperature\;of\;25\;degree\\celsius\;on\;Fahrenheit\\and\;Kelvin\;scale$$

$${\boldsymbol T}_{\mathbf f}\boldsymbol\;\boldsymbol=\boldsymbol\;\frac{\mathbf9}{\mathbf5}\boldsymbol\;{\boldsymbol T}_{\mathbf c}\boldsymbol\;\boldsymbol+\boldsymbol\;\mathbf{32}\\\\T_f\;=\;\frac95\;(25)\;+\;32\\\\T_f\;=\;45\;+\;32\;\\\\{\boldsymbol T}_{\mathbf f}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{77}$$

$${\boldsymbol T}_{\mathbf k}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol T}_{\mathbf c}\boldsymbol\;\boldsymbol+\boldsymbol\;\mathbf{273}\\\\T_k\;=\;25\;+\;273\\\\{\boldsymbol T}_{\mathbf k}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{298}$$

==========================================