9th Physics 2025 Chapter2 Numerical
9th Physics 2025 Chapter2 numerical will be solved. For solution, we can discuss scalar, vector, addition of vectors, types of motion, speed, velocity, acceleration, gravity and their graphs. First, second and third equations of motion will be used to solve the numerical. Value of gravitational acceleration is 10 meters per second square.
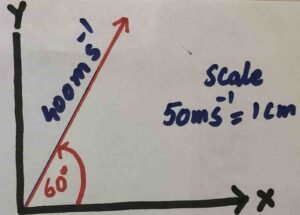
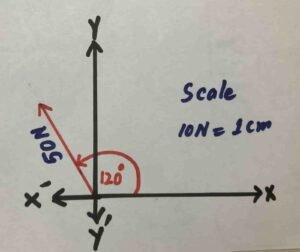
$$2.1\;\;Draw\;the\;\\representative\;line\;of\\the\;following\;vectors:\\(a)\;A\;velocity\;of\\400\;m\;s^{-1}\;making\;an\\angle\;of\;60\;degree\\with\;x-axis.\\(b)\;A\;force\;of\;50\;N\\making\;an\;angle\;of\\120^\circ\;\;with\;x-axis.$$
====================================================================================
$$2.2\;\;\;A\;car\;is\;moving\\with\;an\;average\;speed\\of\;73\;km\;h^{-1}.\;\;How\\much\;time\;will\;it\\take\;to\;cover\;a\\dis\tan ce\;of\;360\;km\;?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Average\mathit\;speed\mathit\;\mathit=\mathit\;v_{\mathit a\mathit v}\mathit=\mathit\;\mathit{72}\mathit\;km\mathit\;h^{\mathit-\mathit1}\\Distance\mathit\;\mathit=\mathit\;S\mathit\;\mathit=\mathit\;\mathit{360}\mathit\;km\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\;S\;=\;v_{av}\;\times\;t\\\\\mathit{360}\mathit\;km\mathit\;\mathit=\mathit\;\mathit{72}\mathit\;km\mathit\;h^{\mathit-\mathit1}\mathit\;\mathit\times\mathit\;t\\\frac{\mathit{360}\mathit\;\mathit k\mathit m}{\mathit{72}\mathit\;\mathit k\mathit m\mathit\;\mathit h^{\mathit-\mathit1}}\mathit\;\mathit=\mathit\;t\\\mathit5\mathit\;h\mathit\;\mathit=\mathit\;t\\t\mathit\;\mathit=\mathit\;\mathit5\mathit\;h\\$$
====================================================================================
$$2.3\;\;\;A\;truck\;starts\\from\;rest.\;It\;reaches\\a\;velocity\;of\;90\;km\;h^{-1}\\in\;50\;seconds.\;Find\\its\;average\;acceleration.\\$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit{90}\mathit\;km\mathit\;h^{\mathit-\mathit1}\\\\\mathit=\mathit\;\mathit{90}\mathit\;\mathit\times\mathit\;\frac{\mathit{1000}}{\mathit{3600}}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;\mathit{90}\mathit\;\mathit\times\mathit\;\mathit0\mathit.\mathit{277}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\\\\mathit\;\mathit=\mathit\;\mathit{24}\mathit.\mathit{93}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit{50}\mathit\;seconds\\\\Average\mathit\;acceleration\mathit\;\mathit=\mathit\;a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol\;\boldsymbol:\boldsymbol-\\a_{av}\;=\;\;\frac{v_f\;-\;v_i}t\\\\a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit\;\frac{\mathit\;\mathit{24}\mathit.\mathit{93}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}\mathit\;\mathit\;\mathit-\mathit\;\mathit0\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}}{\mathit{50}\mathit\;\mathit s}\\\\a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit\;\frac{\mathit\;\mathit{24}\mathit.\mathit{93}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}}{\mathit{50}\mathit\;\mathit s}\\\\a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit0\mathit.\mathit{498}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit0\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\\\\\\\\\$$
====================================================================================
$$2.4\;\;A\;car\;passes\;a\\green\;traffic\;signal\\while\;moving\;with\;a\\velocity\;of\;5\;m\;s^{-1}.\\It\;then\;accelerates\;to\\1.5\;m\;s^{-2}.\;What\;is\;the\\velocity\;of\;car\;after\\5\;seconds?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Acceleration\mathit\;\mathit=\mathit\;a\mathit\;\mathit=\mathit\;\mathit1\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit5\mathit\;seconds\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\v_f\;=\;v_i\;+\;at\\\\v_{\mathit f}\mathit=\mathit\;\mathit\;\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit+\mathit\;\mathit1\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit\;\mathit(\mathit5\mathit\;s\mathit)\\\\v_{\mathit f}\mathit=\mathit\;\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit+\mathit\;\mathit7\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\\\v_{\mathit f}\mathit=\mathit\;\mathit{12}\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\\\\\\\\\$$
====================================================================================
$$2.5\;\;A\;motercycle\\initally\;travelling\;at\\18\;km\;h^{-1}\;accelerates\\at\;cons\tan t\;rate\;of\\2\;m\;s^{-2}.\;How\;far\\will\;the\;motercycle\\go\;in\;10\;seconds?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Initial\mathit\;speed\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit{18}\mathit\;km\mathit\;h^{\mathit-\mathit1}\\\\\mathit=\mathit\;\mathit{18}\mathit\;\mathit\times\frac{\mathit{1000}}{\mathit{3600}}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;\mathit{18}\mathit\;\mathit\times\mathit\;\mathit0\mathit.\mathit{278}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\mathit\;\mathit=\mathit\;\mathit5\mathit.\mathit{004}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Acceleration\mathit\;\mathit=\mathit\;a\mathit\;\mathit=\mathit\;\mathit2\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Time\;=\;t\;=\;10\;s\\\\Dis\tan ce\;=\;s\;=\;?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol s\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf i}\boldsymbol\;\boldsymbol t\boldsymbol\;\boldsymbol+\boldsymbol\;\frac{\mathbf1}{\mathbf2}\boldsymbol\;\boldsymbol a\boldsymbol\;\boldsymbol t^{\mathbf2}\\\\s\mathit\;\mathit=\mathit\;\mathit\;\mathit(\mathit5\mathit.\mathit{004}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit)\mathit\;\mathit(\mathit{10}s\mathit)\mathit\;\mathit+\mathit\;\frac{\mathit1}{\mathit2}\mathit\;\mathit(\mathit2\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;{\mathit(\mathit{10}s\mathit)}^{\mathit2}\\\\s\mathit\;\mathit=\mathit\;\mathit{50}\mathit.\mathit{04}\mathit\;m\mathit\;\mathit+\mathit\;\mathit{100}\mathit\;m\\\\s\mathit\;\mathit=\mathit\;\mathit{150}\mathit.\mathit{04}\mathit\;m$$
====================================================================================
$$2.6\;\;A\;wagon\;is\\moving\;on\;a\;road\\with\;a\;velocity\\of\;54\;km\;h^{-1}.\\Brakes\;are\;applied\\suddenly.\;The\;wagon\\covers\;a\;dis\tan ce\;of\\25\;m\;before\;stopping.\\Determine\;the\;\\acceleration\;of\;the\;wagon.$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit{54}\mathit\;km\mathit\;h^{\mathit-\mathit1}\\\\\mathit=\mathit{54}\mathit\;\mathit\times\mathit\;\frac{\mathit{1000}}{\mathit{3600}}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;\mathit{54}\mathit\;\mathit\times\mathit\;\mathit0\mathit.\mathit{278}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\mathit=\mathit\;\mathit{15}\mathit.\mathit{012}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Distance\mathit\;\mathit=\mathit\;S\mathit\;\mathit=\mathit\;\mathit{25}\mathit\;m\\\\Acceleration\mathit\;\mathit=\mathit\;a\mathit\;\mathit=\mathit\;\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\mathbf2\boldsymbol a\boldsymbol S\boldsymbol\;\boldsymbol=\boldsymbol\;{\mathbf v}_{\mathbf f}^{\mathbf2}\boldsymbol\;\boldsymbol-\boldsymbol\;{\mathbf v}_{\mathbf i}^{\mathbf2}\\\\\mathit2a\mathit(\mathit{25}m\mathit)\mathit\;\mathit=\mathit\;\mathit0^{\mathit2}\mathit\;\mathit-\mathit\;{\mathit(\mathit{15}\mathit.\mathit{012}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit)}^{\mathit2}\\\\a\mathit\;\mathit=\mathit\;\frac{\mathit-\mathit{225}\mathit.\mathit{36}\mathit\;\mathit m^{\mathit2}\mathit\;\mathit s^{\mathit-\mathit2}}{\mathit{50}\mathit m}\\\\a\mathit\;\mathit=\mathit\;\mathit-\mathit4\mathit.\mathit{507}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\$$
====================================================================================
$$2.7\;\;A\;stone\;is\;dropped\\from\;a\;height\;of\;45\;m.\\How\;long\;will\;it\;take\;to\\reach\;the\;ground\;?\;What\\will\;be\;its\;velocity\;just\\before\;hitting\;the\;ground\;?\\\\$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Height\mathit\;\mathit=\mathit\;h\mathit\;\mathit=\mathit\;\mathit{45}\mathit\;m\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit?\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol h\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol v{\boldsymbol i}_{\mathbf t}\boldsymbol\;\boldsymbol+\boldsymbol\;\frac{\mathbf1}{\mathbf2}\boldsymbol\;\boldsymbol g\boldsymbol\;\boldsymbol t^{\mathbf2}\\\\\mathit{45}\mathit\;m\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit(t\mathit\;seconds\mathit)\mathit\;\mathit+\frac{\mathit1}{\mathit2}\mathit(\mathit{10}\mathit\;\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;\mathit(t^{\mathit2}\mathit)\\\\\mathit{45}\mathit\;m\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;\mathit+\mathit(\mathit\;\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;\mathit(t^{\mathit2}\mathit)\\\\\frac{\mathit{45}\mathit\;\mathit m}{\mathit5\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit2}}\mathit=\mathit\;t^{\mathit2}\\\\\mathit9\mathit\;s^{\mathit2}\mathit\;\mathit=\mathit\;t^{\mathit2}\\\\Taking\mathit\;square\mathit\;root\mathit\;on\mathit\;both\mathit\;side\\\\t\mathit\;\mathit=\mathit\;\mathit3\mathit\;s\\\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\boldsymbol\;\\{\boldsymbol v}_{\mathbf f}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf i}\boldsymbol\;\boldsymbol+\boldsymbol\;\boldsymbol a\boldsymbol\;\boldsymbol t\\\\v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;\mathit+\mathit\;\mathit(\mathit3\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;\mathit(\mathit{10}s\mathit)\\\\v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}$$
====================================================================================
$$2.8\;\;A\;car\;travels\\10\;km\;with\;an\\average\;velocity\;of\\20\;m\;s^{-1}.\;Then\;it\\travels\;in\;the\;same\\direction\;through\;a\\diversion\;at\;an\\average\;velocity\;of\\4\;m\;s^{-1}\;for\;the\;next\\0.8\;km.\;Determine\;the\\average\;velocity\;of\;the\\car\;for\;the\;total\;journey.$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Distance\mathit\;\mathit=\mathit\;S_{\mathit1}\mathit\;\mathit=\mathit\;\mathit{10}\mathit\;km\mathit\;\mathit=\mathit\;\mathit{10}\mathit\;\mathit\times\mathit\;\mathit{1000}\mathit\;m\\\mathit=\mathit\;\mathit{10000}\mathit\;m\\\\Average\mathit\;velocity\mathit\;\mathit=\mathit\;v{\mathit1}_{\mathit a\mathit v}\mathit=\mathit\;\mathit{20}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\time\mathit\;\mathit=\mathit\;t_{\mathit1}\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\{\boldsymbol S}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol v{\mathbf1}_{\mathbf a\mathbf v}\boldsymbol\;\boldsymbol\times\boldsymbol\;{\boldsymbol t}_{\mathbf1}\\\\\mathit{10000}\mathit\;m\mathit\;\mathit=\mathit\;\mathit{20}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit\times\mathit\;\mathit\;t_{\mathit1}\\\\\frac{\mathit{10000}\mathit\;\mathit m}{\mathit{20}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}}\mathit\;\mathit=\mathit\;t_{\mathit1}\\\\t_{\mathit1}\mathit\;\mathit=\mathit\;\mathit{500}\mathit\;s\\\\\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Distance\mathit\;\mathit=\mathit\;S_{\mathit2}\mathit\;\mathit=\mathit\;\mathit0\mathit.\mathit8\mathit\;km\mathit\;\mathit=\mathit\;\mathit0\mathit.\mathit8\mathit\;\mathit\times\mathit\;\mathit{1000}\mathit\;m\\\mathit=\mathit\;\mathit{800}\mathit\;m\\\\Average\mathit\;velocity\mathit\;\mathit=\mathit\;v{\mathit2}_{\mathit a\mathit v}\mathit=\mathit\;\mathit4\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\time\mathit\;\mathit=\mathit\;t_{\mathit2}\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\{\boldsymbol S}_{\mathbf2}\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol v{\mathbf2}_{\mathbf a\mathbf v}\boldsymbol\;\boldsymbol\times\boldsymbol\;{\boldsymbol t}_{\mathbf2}\\\\\mathit{800}m\mathit\;\mathit=\mathit\;\mathit4\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit\times\mathit\;\mathit\;t_{\mathit2}\\\\\frac{\mathit{800}\mathit\;\mathit m}{\mathit4\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}}\mathit\;\mathit=\mathit\;t_{\mathit2}\\\\\mathit\;t_{\mathit2}\mathit\;\mathit=\mathit\;\mathit{200}\mathit\;s\\\\t\mathit\;\mathit=\mathit\;t_{\mathit1}\mathit\;\mathit+\mathit\;t_{\mathit2}\\\\t\mathit\;\mathit=\mathit\;\mathit{500}\mathit\;m\mathit\;\mathit+\mathit\;\mathit{200}\mathit\;m\\\\t\mathit\;\mathit=\mathit\;\mathit{700}\mathit\;s\\\\\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Distance\mathit\;\mathit=\mathit\;S\mathit\;\mathit=\mathit?\\\\time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit{700}\mathit\;s\\\\Average\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit?\\\\Distance\mathit\;\mathit=\mathit\;S\mathit\;\mathit=S_{\mathit1}\mathit+\mathit\;S_{\mathit2}\mathit\;\mathit=\mathit\;\mathit{10000}m\mathit+\mathit{800}m\\\mathit=\mathit\;\mathit{10800}m\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol S\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf a\mathbf v}\boldsymbol\;\boldsymbol\times\boldsymbol\;\boldsymbol t\\\\\mathit{10800}\mathit\;m\mathit\;\mathit=\mathit\;v_{\mathit a\mathit v}\mathit\;\mathit\times\mathit\;\mathit{700}\mathit\;s\\\\\frac{\mathit{10800}\mathit\;\mathit m\mathit\;}{\mathit{700}\mathit\;\mathit s}\mathit\;\mathit=\mathit\;\mathit\;v_{\mathit a\mathit v}\\\\\mathit\;v_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit{15}\mathit.\mathit{428}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\\\\\\$$
====================================================================================
$$2.9\;\;A\;ball\;is\;dropped\\from\;the\;top\;of\;a\\tower.\;The\;ball\\reaches\;the\;ground\\in\;5\;seconds.\;Find\\height\;of\;the\;tower\;\\and\;velocity\;of\;the\\ball\;with\;which\;it\\strikes\;the\;ground.\;$$
$$\;\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\boldsymbol\;\\\\Time\mathit\;\mathit=\mathit\;\mathit5\mathit\;seconds\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Gravitional\mathit\;accelerational\mathit\;\mathit=\mathit\;g\mathit\;\mathit=\mathit\;\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Height\mathit\;\mathit=\mathit\;h\mathit\;\mathit=\mathit\;\mathit?\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol h\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol v}_{\boldsymbol i}\boldsymbol{\mathit\;}\boldsymbol t\boldsymbol{\mathit\;}\boldsymbol{\mathit+}\boldsymbol{\mathit\;}\frac{\boldsymbol1}{\boldsymbol2}\boldsymbol{\mathit\;}\boldsymbol g\boldsymbol{\mathit\;}\boldsymbol t^{\boldsymbol2}\\\\h\;=\;(0\;m\;s^{-1})\;(5\;s)\;+\;\frac12\;(10\;m\;s^{-2})\;{(5\;s)}^2\\\\h\;=\;0\;m\;+\;125\;m\\\\h\;=\;125\;m\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\{\boldsymbol v}_{\mathbf f}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf i}\boldsymbol\;\boldsymbol+\boldsymbol\;\boldsymbol g\boldsymbol\;\boldsymbol t\\\\\\v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit+\mathit\;\mathit(\mathit\;\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;\mathit(\mathit\;\mathit5\mathit\;s\mathit\;\mathit)\\\\v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit+\mathit\;\mathit{50}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit{50}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\\\\\\\\\\$$
====================================================================================
$$2.10\;\;A\;cricket\;ball\\is\;hit\;so\;that\;it\\travels\;straight\;up\\in\;the\;air.\;An\\observer\;notes\;that\\it\;took\;3\;seconds\\to\;reach\;the\;highest\\point.\;What\;was\;the\\initial\;velocity\;of\;the\\ball\;?\;If\;the\;ball\;was\\hit\;1\;m\;above\;the\\ground,\;how\;high\;did\\it\;rise\;from\;\;the\;ground\;?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit3\mathit\;seconds\\\\Gravitional\mathit\;acceleration\mathit\;\mathit=\mathit\;g\mathit\;\mathit=\mathit\;\mathit-\mathit\;\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol v}_{\boldsymbol f}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol v}_{\boldsymbol i}\boldsymbol{\mathit\;}\boldsymbol{\mathit+}\boldsymbol{\mathit\;}\boldsymbol g\boldsymbol{\mathit\;}\boldsymbol t\\\\\\\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit+\mathit\;\mathit(\mathit\;\mathit-\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;\mathit(\mathit\;\mathit3\mathit\;s\mathit\;\mathit)\\\\\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit\;\mathit-\mathit\;\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\\\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\\\Initial\mathit\;height\mathit\;\mathit=\mathit\;h_{\mathit1}\mathit\;\mathit=\mathit\;\mathit1\mathit\;m\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Gravitional\mathit\;acceleration\mathit\;\mathit=\mathit\;g\mathit\;\mathit=\mathit\;\mathit-\mathit\;\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Height\mathit\;\mathit=\mathit\;h_{\mathit2}\mathit\;\mathit=\mathit\;\mathit?\\\\Total\mathit\;height\mathit\;\mathit=\mathit\;h\mathit\;\mathit=\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\mathbf2\boldsymbol g{\boldsymbol h}_{\mathbf2}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol({\boldsymbol v}_{\mathbf f}\boldsymbol)}^{\mathbf2}\boldsymbol\;\boldsymbol-\boldsymbol\;{\boldsymbol({\mathbf v}_{\mathbf i}\boldsymbol)}^{\mathbf2}\\\\\\\mathit2\mathit\;\mathit(\mathit\;\mathit-\mathit\;\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit\;\mathit)\mathit\;h_{\mathit2}\mathit\;\mathit=\mathit\;\mathit\;{\mathit(\mathit\;\mathit0\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}\mathit)}^{\mathit2}\mathit\;\mathit-\mathit\;{\mathit(\mathit{30}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}\mathit)}^{\mathit2}\\\\\mathit\;\mathit(\mathit\;\mathit-\mathit\;\mathit{20}\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit\;\mathit)\mathit\;h_{\mathit2}\mathit\;\mathit=\mathit\;\mathit-\mathit\;{\mathit(\mathit{30}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}\mathit)}^{\mathit2}\\\\h_{\mathit2}\mathit\;\mathit=\mathit\;\frac{\mathit{900}\mathit\;\mathit m^{\mathit2}\mathit\;\mathit s^{\mathit-\mathit2}}{\mathit{20}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit2}}\\\\h_{\mathit2}\mathit\;\mathit=\mathit\;\mathit{45}\mathit\;m\\\\h\mathit\;\mathit=\mathit\;h_{\mathit1}\mathit\;\mathit+\mathit\;h_{\mathit2}\\\\h\mathit\;\mathit=\mathit\;\mathit1m\mathit\;\mathit+\mathit\;\mathit{45}m\\\\h\mathit\;\mathit=\mathit\;\mathit{46}m\\\\\\\\\\\\\\\\\\\\\\\\\\$$
Check! Some useful links below.
Class 9 Physics new book 2025 chapter 4 Numerical
You tube channel Sir Najam
Home Page Notespunjab.com
