Revised Syllabus 9th Class Physics Numerical
Revised Syllabus 9th Class Physics Numerical solution
Chapter 1
1.2 State the answers of problem 1.1 in scientific notation
Number of minutes in 1 hour = 60
seconds in 1 hour = (60) (60) = 3600
Its mean seconds in 1 day = (3600) (24) = 86,400 = $$8.64\;\times\;10^4$$
seconds in a week = (86,400) (7) = 604,800 = $$6.048\;\times\;10^5$$
seconds in 1 month = (86,400)(30) = 2,592,000 = $$2.592\;\times\;10^6$$
==========================================
1.5 Calculate the following. State your answer in scientific notation.
$$\frac{(3\times10^2kg)\times(4.0km)}{5\times10^2\;s^2}\\\\\frac{12}5kg\;km\;s^{-2}\\\\2.4\;kg\;km\;s^{-2}\\\\2.4\;\times\;1000\;kg\;m\;s^{-2}\\\\2.4\;\times10^3\;kg\;m\;s^{-2}\\\\$$
==========================================
1.7 Write in scientific notation
$$(a)\;\;0.0035m\\\\=\;3.5\;\times\;10^{-3}\;m\\\\\\(b)\;\;206.4\;\times10^2\;m\\\\=\;2.064\;\times\;10^2\;\times\;10^2\;m\\\\=\;2.064\;\times\;10^{2+2}\;m\\\\=\;2.064\;\times\;10^4\;m\\\\$$
==========================================
1.9
$$Light\;year\;is\;a\;unit\;used\\in\;Astronomy.\;It\;is\;the\\dis\tan ce\;covered\;by\\light\;in\;one\;year.\\Taking\;the\;speed\;of\;light\\as\;3.0\times10^8\;m\;s^{-1},\\calculate\;the\;dis\tan ce\;$$
$$Number\;of\;seconds\;in\;one\;minute\\=\;60\\\\Number\;of\;seconds\;in\;one\;hour\;\\=\;60\;\times\;60\\\\Number\;of\;seconds\;in\;one\;day\;\\=\;60\;\times\;60\;\times\;24\\\\number\;of\;seconds\;in\;one\;year\;\\=\;60\times60\times24\times365\\\\Number\;of\;seconds\;in\;one\;year\\\;=\;31,536,000\\\\Dis\tan ce=31,536,000\times3.0\times10^8m\\=\;94,608,000\;\times\;10^8\;m\\=\;9.4608\;\times\;10^7\;\times\;10^8\;m\\=\;9.4608\;\times\;10^{7+8}\;m\\=\;9.4608\;\times\;10^{15}\;m$$
==========================================
Chapter 2
$$2.5\;\;A\;motercycle\\initally\;travelling\;at\\18\;km\;h^{-1}\;accelerates\\at\;cons\tan t\;rate\;of\\2\;m\;s^{-2}.\;How\;far\\will\;the\;motercycle\\go\;in\;10\;seconds?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Initial\mathit\;velociy\mathit\;\mathit=\mathit\;v_i\mathit\;\mathit=\mathit\;\mathit{18}\mathit\;km\mathit\;h^{\mathit-\mathit1}\\\\\mathit=\mathit\;\mathit{18}\mathit\;\mathit\times\frac{\mathit{1000}}{\mathit{3600}}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\\mathit=\mathit\;\mathit{18}\mathit\;\mathit\times\mathit\;\mathit0\mathit.\mathit{278}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\mathit\;\mathit=\mathit\;\mathit5\mathit.\mathit{004}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Acceleration\mathit\;\mathit=\mathit\;a\mathit\;\mathit=\mathit\;\mathit2\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Time\;=\;t\;=\;10\;s\\\\Dis\tan ce\;=\;s\;=\;?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol s\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf i}\boldsymbol\;\boldsymbol t\boldsymbol\;\boldsymbol+\boldsymbol\;\frac{\mathbf1}{\mathbf2}\boldsymbol\;\boldsymbol a\boldsymbol\;\boldsymbol t^{\mathbf2}\\\\s\mathit=\mathit(\mathit5\mathit.\mathit{004}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit)\mathit\;\mathit(\mathit{10}s\mathit)\mathit\;\mathit+\frac{\mathit1}{\mathit2}\mathit(\mathit2\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;{\mathit(\mathit{10}s\mathit)}^{\mathit2}\\\\s\mathit\;\mathit=\mathit\;\mathit{50}\mathit.\mathit{04}\mathit\;m\mathit\;\mathit+\mathit\;\mathit{100}\mathit\;m\\\\s\mathit\;\mathit=\mathit\;\mathit{150}\mathit.\mathit{04}\mathit\;m$$
====================================================================================
$$2.8\;\;A\;car\;travels\\10\;km\;with\;an\\average\;velocity\;of\\20\;m\;s^{-1}.\;Then\;it\\travels\;in\;the\;same\\direction\;through\;a\\diversion\;at\;an\\average\;velocity\;of\\4\;m\;s^{-1}\;for\;the\;next\\0.8\;km.\;Determine\;the\\average\;velocity\;of\;the\\car\;for\;the\;total\;journey.$$
$$Data:-\\\\Distance\mathit\;\mathit=\mathit\;S_{\mathit1}\mathit\;\mathit=\mathit\;\mathit{10}\mathit\;km\mathit\;\mathit=\mathit\;\mathit{10}\mathit\;\mathit\times\mathit\;\mathit{1000}\mathit\;m\\\mathit=\mathit\;\mathit{10000}\mathit\;m\\\\Average\mathit\;velocity\mathit\;\mathit=\mathit\;v{\mathit1}_{av}\mathit=\mathit\;\mathit{20}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\time\mathit\;\mathit=\mathit\;t_{\mathit1}\mathit\;\mathit=\mathit\;\mathit?\\\\Formula:-\\{\boldsymbol S}_1\boldsymbol\;\boldsymbol={{\mathbf v}_1}_{\mathbf{av}}\boldsymbol\;\boldsymbol\times\boldsymbol\;{\boldsymbol t}_1\\\\\mathit{10000}\mathit\;m\mathit\;\mathit=\mathit\;\mathit{20}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit\times\mathit\;\mathit\;t_{\mathit1}\\\\\frac{\mathit{10000}\mathit\;m}{\mathit{20}\mathit\;m\mathit\;s^{\mathit-\mathit1}}\mathit\;\mathit=\mathit\;t_{\mathit1}\\\\t_{\mathit1}\mathit\;\mathit=\mathit\;\mathit{500}\mathit\;s\\\\Data:-\\\\Distance\mathit\;\mathit=\mathit\;S_{\mathit2}\mathit\;\mathit=\mathit\;\mathit0\mathit.\mathit8\mathit\;km\mathit\;\mathit=\mathit\;\mathit0\mathit.\mathit8\mathit\;\mathit\times\mathit\;\mathit{1000}\mathit\;m\\\mathit=\mathit\;\mathit{800}\mathit\;m\\\\Average\mathit\;velocity\mathit\;\mathit=\mathit\;v{\mathit2}_{av}\mathit=\mathit\;\mathit4\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\time\mathit\;\mathit=\mathit\;t_{\mathit2}\mathit\;\mathit=\mathit\;\mathit?\\\\Formula:-\\{\boldsymbol S}_{\mathbf2}\boldsymbol\;\boldsymbol={{\mathbf v}_{\mathbf2}}_{\mathbf{av}}\boldsymbol\;\boldsymbol\times\boldsymbol\;{\boldsymbol t}_{\mathbf2}\\\\\mathit{800}m\mathit\;\mathit=\mathit\;\mathit4\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit\times\mathit\;\mathit\;t_{\mathit2}\\\\\frac{\mathit{800}\mathit\;m}{\mathit4\mathit\;m\mathit\;s^{\mathit-\mathit1}}\mathit\;\mathit=\mathit\;t_{\mathit2}\\\\\mathit\;t_{\mathit2}\mathit\;\mathit=\mathit\;\mathit{200}\mathit\;s\\\\t\mathit\;\mathit=\mathit\;t_{\mathit1}\mathit\;\mathit+\mathit\;t_{\mathit2}\\\\t\mathit\;\mathit=\mathit\;\mathit{500}\mathit\;s\mathit\;\mathit+\mathit\;\mathit{200}\mathit\;s\\\\t\mathit\;\mathit=\mathit\;\mathit{700}\mathit\;s\\\\Data:-\\\\Distance\mathit\;\mathit=\mathit\;S\mathit\;\mathit=\mathit?\\\\time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit{700}\mathit\;s\\\\Average\mathit\;velocity\mathit\;\mathit=\mathit\;v_{av}\mathit\;\mathit=\mathit\;\mathit?\\\\Distance\mathit\;\mathit=\mathit\;S\mathit\;\mathit=S_{\mathit1}\mathit+\mathit\;S_{\mathit2}\mathit\;\mathit=\mathit\;\mathit{10000}m\mathit+\mathit{800}m\\\mathit=\mathit\;\mathit{10800}m\\\\\\Formula:-\\\boldsymbol S\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf a\mathbf v}\boldsymbol\;\boldsymbol\times\boldsymbol\;\boldsymbol t\\\\\mathit{10800}\mathit\;m\mathit\;\mathit=\mathit\;v_{av}\mathit\;\mathit\times\mathit\;\mathit{700}\mathit\;s\\\\\frac{\mathit{10800}\mathit\;m\mathit\;}{\mathit{700}\mathit\;s}\mathit\;\mathit=\mathit\;\mathit\;v_{av}\\\\\mathit\;v_{av}\mathit\;\mathit=\mathit\;\mathit{15}\mathit.\mathit{428}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\$$
====================================================================================
$$2.10\;\;A\;cricket\;ball\\is\;hit\;so\;that\;it\\travels\;straight\;up\\in\;the\;air.\;An\\observer\;notes\;that\\it\;took\;3\;seconds\\to\;reach\;the\;highest\\point.\;What\;was\;the\\initial\;velocity\;of\;the\\ball\;?\;If\;the\;ball\;was\\hit\;1\;m\;above\;the\\ground,\;how\;high\;did\\it\;rise\;from\;\;the\;ground\;?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit3\mathit\;seconds\\\\Gravitional\mathit\;acceleration\mathit=g\mathit=\mathit-\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_f\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_i\mathit\;\mathit=\mathit\;\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol v}_{\boldsymbol f}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol v}_{\boldsymbol i}\boldsymbol{\mathit\;}\boldsymbol{\mathit+}\boldsymbol{\mathit\;}\boldsymbol g\boldsymbol{\mathit\;}\boldsymbol t\\\\\\\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;v_i\mathit\;\mathit+\mathit\;\mathit(\mathit\;\mathit-\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;\mathit(\mathit\;\mathit3\mathit\;s\mathit\;\mathit)\\\\\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;v_i\mathit\;\mathit\;\mathit-\mathit\;\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\mathit\;v_i\mathit\;\mathit=\mathit\;\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\\\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\\\Initial\mathit\;height\mathit\;\mathit=\mathit\;h_{\mathit1}\mathit\;\mathit=\mathit\;\mathit1\mathit\;m\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_i\mathit\;\mathit=\mathit\;\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_f\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Gravitional\mathit\;acceleration\mathit=g\mathit=\mathit-\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Height\mathit\;\mathit=\mathit\;h_{\mathit2}\mathit\;\mathit=\mathit\;\mathit?\\\\Total\mathit\;height\mathit\;\mathit=\mathit\;h\mathit\;\mathit=\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\mathbf2\boldsymbol g{\boldsymbol h}_{\mathbf2}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol({\boldsymbol v}_{\mathbf f}\boldsymbol)}^{\mathbf2}\boldsymbol\;\boldsymbol-\boldsymbol\;{\boldsymbol({\mathbf v}_{\mathbf i}\boldsymbol)}^{\mathbf2}\\\\\\\mathit2\mathit(\mathit-\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit\;\mathit)\mathit\;h_{\mathit2}\mathit={\mathit(\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit)}^{\mathit2}\mathit-{\mathit(\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit)}^{\mathit2}\\\\\mathit\;\mathit(\mathit\;\mathit-\mathit\;\mathit{20}\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit\;\mathit)\mathit\;h_{\mathit2}\mathit\;\mathit=\mathit\;\mathit-\mathit\;{\mathit(\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit)}^{\mathit2}\\\\h_{\mathit2}\mathit\;\mathit=\mathit\;\frac{\mathit{900}\mathit\;m^{\mathit2}\mathit\;s^{\mathit-\mathit2}}{\mathit{20}\mathit\;m\mathit\;s^{\mathit-\mathit2}}\\\\h_{\mathit2}\mathit\;\mathit=\mathit\;\mathit{45}\mathit\;m\\\\h\mathit\;\mathit=\mathit\;h_{\mathit1}\mathit\;\mathit+\mathit\;h_{\mathit2}\\\\h\mathit\;\mathit=\mathit\;\mathit1m\mathit\;\mathit+\mathit\;\mathit{45}m\\\\h\mathit\;\mathit=\mathit\;\mathit{46}m\\\\\\$$
====================================================================================
Chapter 3
$$\boldsymbol3\boldsymbol{\mathit.}\boldsymbol5\;\;\;A\;astronaut\;weighs\\70\;kg.\;He\;throws\;a\;wrench\\of\;mass\;300\;g\;at\;a\;speed\\of\;3.5\;m\;s^{-1}.\;Determine:\\(a)\;\;the\;speed\;of\;astronaut\\as\;he\;recoils\;away\;from\\the\;wrench\\(b)\;\;the\;dis\tan ce\;covered\;by\\the\;astronaut\;in\;30\;minutes$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;of\;astronaut\;=\;m_1\;\;\;=\;70\;kg\\Mass\;of\;wrench\;=\;m_2\;\;\;=\;300\;g\;=\;0.3\;kg\\Speed\;of\;astronaut\;=\;v_1\;\;\;=\;?\\Speed\;of\;wrench\;=\;v_2\;\;\;=\;3.5\;m\;s^{-1}\\\\Law\mathit\;of\mathit\;conservation\mathit\;of\mathit\;momentum\\states\;that\mathit\;momentum\mathit\;before\mathit\;the\\collision\mathit\;is\;equal\mathit\;to\mathit\;the\mathit\;momentum\\after\mathit\;the\mathit\;collision$$
$$m_1\;u_1\;+\;m_2\;u_2\;=\;m_1\;v_1\;+\;m_2\;v_2\;\\\\Here\\Momentum\;before\;the\;collision\;is\;zero\\\\so\\m_1\;u_1\;+\;m_2\;u_2\;=\;0\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol m}_{\boldsymbol1}\boldsymbol{\mathit\;}{\boldsymbol u}_{\boldsymbol1}\boldsymbol{\mathit\;}\boldsymbol{\mathit+}\boldsymbol{\mathit\;}{\boldsymbol m}_{\boldsymbol2}\boldsymbol{\mathit\;}{\boldsymbol u}_{\boldsymbol2}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol m}_{\boldsymbol1}\boldsymbol{\mathit\;}{\boldsymbol v}_{\boldsymbol1}\boldsymbol{\mathit\;}\boldsymbol{\mathit+}\boldsymbol{\mathit\;}{\boldsymbol m}_{\boldsymbol2}\boldsymbol{\mathit\;}{\boldsymbol v}_{\boldsymbol2}\boldsymbol{\mathit\;}\\\\0=\;m_1\;v_1\;+\;m_2\;v_2\;\\\\m_1\;v_1\;=\;-\;m_2\;v_2\;\\\\v_1\;=\;\frac{-\;m_2\;v_2}{m_1}\\\\v_1\;=\;\frac{-\;(0.3\;kg\;)\;(\;3.5\;m\;s^{-1}\;)}{70\;kg}\\\\v_1\;=\;0.015\;m\;s^{-1}\;\\\\v_1\;=\;1.5\;\times10^{-2}\;m\;s^{-1}$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Time\;=\;t\;=\;30\;min\;=\;30\times60\;=\;1800\;s\\\\Speed\;of\;astronaut\;=\;v\;=\;0.015\;m\;s^{-1}\\\\Dis\tan ce\;by\;astronaut\;=\;S\;=\;?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol S\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol v\boldsymbol{\mathit\;}\boldsymbol t\\\\S\;=\;(1800\;s\;)\;(\;0.015\;m\;s^{-1}\;)\\S\;=\;27\;m$$
=======================================
$$\boldsymbol3\boldsymbol{\mathit.}\boldsymbol6\;\;\;\;A\;6.5\;\times\;10^3\;kg\;bogie\;of\\a\;goods\;train\;is\;moving\;with\\a\;velocity\;of\;\;0.8\;m\;s^{-1}.\\Another\;bogie\;of\;mass\;\\9.2\;\times\;10^3\;kg\;coming\;from\\behind\;with\;a\;velocity\;of\\1.2\;m\;s^{-1}\;collides\;with\\the\;first\;one\;and\;couples\\it.\;Find\;the\;common\;velocity\\of\;the\;two\;bogies\;after\;they\\become\;coupled.$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;of\;1st\;bogie\;=\;m_1\;=\;6.5\;\times10^3\;kg\\Velocity\;of\;1st\;bogie\;=\;v_1\;=\;0.8\;m\;s^{-1}\\Mass\;of\;2nd\;bogie\;=\;m_2\;=\;9.2\;\times10^3\;kg\\Velocity\;of\;2nd\;bogie\;=\;v_2\;=\;1.2\;m\;s^{-1}\\Common\;velocity\;=\;v\;=\;?$$
$$Formula\mathit:\mathit-\\m_{\mathit1}\mathit\;v_{\mathit1}\mathit\;\mathit+\mathit\;m_{\mathit2}\mathit\;v_{\mathit2}\mathit\;\mathit=\mathit\;\mathit(\mathit\;m_{\mathit1}\mathit\;\mathit+\mathit\;m_{\mathit2}\mathit\;\mathit)\mathit\;v\\\\\frac{m_1\;v_1\;+\;m_2\;v_2}{m_1\;+\;m_2}\;=\;v\\\\v\;=\;\frac{m_1\;v_1\;+\;m_2\;v_2}{m_1\;+\;m_2}\\\\v=\frac{(6.5\times10^3)(0.8)+(9.2\times10^3)(1.2)}{6.5\;\times10^3\;+\;9.2\;\times10^3\;}\\\\v\;=\;\frac{10^3\;(\;6.5\;\times\;0.8\;\;+\;9.2\;\times\;1.2\;)}{10^3\;\;(\;6.5\;+\;9.2\;)}\\\\v\;=\;\frac{5.2\;\;+\;11.04\;}{15.7}\\\\v\;=\;\frac{16.24\;}{15.7}\\\\v\;=\;1.03\;m\;s^{-1}$$
========================================
$$\boldsymbol3\boldsymbol{\mathit.}\boldsymbol8\;\;\;\;A\;ball\;of\;mass\;0.4\;kg\\is\;dropped\;on\;the\;floor\;from\\a\;height\;of\;1.8\;m.\;The\;ball\\rebounds\;straight\;upward\;to\\a\;height\;of\;0.8\;m.\;What\;is\\the\;magnitude\;and\;direction\\of\;the\;impulse\;applied\;to\\the\;ball\;by\;the\;floor$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\Mass\;=\;m\;=\;0.4\;kg\\Initial\;height\;=\;h_1\;=\;1.8\;m\\Rebound\;height\;=\;h_2\;=\;0.8\;m\\Impulse\;=\;J\;=\;?\\\\\\\\\\\\\\$$
$$Velocity\;before\;touching\;the\;ground\;is\;V_f\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\mathbf2\boldsymbol\;\boldsymbol g\boldsymbol\;\boldsymbol h\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol({\boldsymbol V}_{\mathbf f}\boldsymbol)}^{\mathbf2}\boldsymbol\;\boldsymbol-{\boldsymbol({\mathbf V}_{\mathbf i}\boldsymbol)}^{\mathbf2}\boldsymbol\;\\\\2\;(\;10\;m\;s^{-2}\;)\;(\;1.8\;m\;)\;=\;\;{(V_{\mathrm f})}^2\;-\;0\\\\36\;m^2\;s^{-2}\;=\;\;{(V_{\mathrm f})}^2\;\\\\V_f\;=\;6\;m\;s^{-1}\\$$
$$Impulse\;is\;a\;vector\;quantity\;\\Hence\;direction\;matters\\Because\;the\;ball\;is\;moving\\downward.\\\\V_f\;=\;-\;6\;m\;s^{-1}\\Initial\;momentum\;=\;P_1\;=\;?\;\\\\P\;=\;m\;v\\\\P_1\;=\;(\;0.4\;kg\;)\;(\;-6\;m\;s^{-1}\;)\\\\P\;=\;-\;2.4\;N\;s\\\\\\\\$$
$$At\;the\;maximum\;height\;V_f\;=\;0\\2\;g\;h\;=\;{(v_f)}^2\;-\;{(v_i)}^2\\\\2\;(\;10\;m\;s^{-2}\;)\;(\;0.8\;m\;)\;=\;0\;-\;{(v_i)}^2\\\\16\;m^2\;s^{-2}\;=\;{(v_i)}^2\\\\v_i\;=\;4\;m\;s^{-1}\\\\Ball\;is\;going\;upward,\;So\\v_{\mathrm i}\;=+\;\;4\;m\;s^{-1}\\\\Final\;momentum\;=\;P_2\;=\;?\\\\P_2\;=(0.4\;kg\;)\;(\;4\;m\;s^{-1}\;)\\\\P\;=\;1.6\;Ns$$
$$Change\;in\;momontum\;is\;equal\;to\;the\\final\;momentum\;minus\;initial\;momentum\\\\\triangle P\;=\;P_f\;-\;P_i\;\\\\\triangle P\;=\;\;1.6\;Ns\;-\;(\;-\;2.4\;Ns\;)\\\\\triangle P\;=\;1.6\;Ns\;+\;2.4\;Ns\;\\\\\triangle P\;=\;4\;Ns\\$$
$$Total\;Change\;in\;momontum\\is\;called\;Impulse.\\\\So\\J\;=\;\triangle P\\\\J\;=\;4\;Ns\\$$
========================================
$$\boldsymbol3\boldsymbol{\mathit.}\boldsymbol9\;\;\;Two\;balls\;of\;masses\\0.2\;kg\;and\;0.4\;kg\;are\\moving\;towards\;each\;other\\with\;velocities\;20\;m\;s^{-1}\\and\;5\;m\;s^{-1}\;respectively.\\After\;collision,\;the\;velocity\\of\;0.2\;kg\;ball\;becomes\\6\;m\;s^{-1}.\;What\;will\;be\\the\;velocity\;of\;0.4\;kg\\ball\;?\\$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;of\;1st\;ball\;=\;m_1\;=\;0.2\;kg\\Mass\;of\;2nd\;ball\;=\;m_2\;=\;0.4\;kg\\Velocity\;of\;m_1\;before\;collision\\=u_1=20\;m\;s^{-1}\\Velocity\;of\;m_2\;before\;collision\\=u_2=\;-5\;m\;s^{-1}\\Velocity\;of\;m_1\;after\;collision\\=v_1=6\;m\;s^{-1}\\Velocity\;of\;m_2\;after\;collision\\=v_2=?\\$$
$$Law\mathit\;of\mathit\;conservation\mathit\;of\mathit\;momentum\\states\mathit\;that\mathit\;momentum\mathit\;before\mathit\;the\\collision\mathit\;is\mathit\;equal\mathit\;to\mathit\;the\mathit\;momentum\\after\mathit\;the\mathit\;collision\mathit.\\\\m_{\mathit1}\mathit\;u_{\mathit1}\mathit\;\mathit+\mathit\;m_{\mathit2}\mathit\;u_{\mathit2}\mathit\;\mathit=\mathit\;m_{\mathit1}\mathit\;v_{\mathit1}\mathit\;\mathit+\mathit\;m_{\mathit2}\mathit\;v_{\mathit2}\boldsymbol{\mathit\;}$$
$$m_1\;u_1\;+\;m_2\;u_2\;-\;m_1\;v_1\;=\;\;m_2\;v_2\\\\\frac{m_1\;u_1\;+\;m_2\;u_2\;-\;m_1\;v_1}{m_2}=\;v_2\\\\v_2=\frac{(0.2)(20)+(0.4)(-5)-(0.2)(6)}{0.4\;}\\\\v_2\;=\;\frac{4\;-\;2\;-1.2\;}{0.4\;}\\\\v_2\;=\;\frac{0.8\;}{0.4\;}\\\\v_2\;=\;2\;m\;s^{-1}$$
========================================
Chapter 4
$$4.2\;\;\;A\;force\;of\;300\;N\;is\\applied\;perpendicularly\;at\\the\;knob\;of\;a\;door\;to\;open\\it.\;If\;knob\;is\;1.2\;m\;away\\from\;the\;hinge,\;what\;is\;the\\torque\;applied\;?\;Is\;it\\positive\;or\;negative\;torque?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Force\mathit\;\mathit=\mathit\;F\mathit\;\mathit=\mathit\;\mathit{300}\mathit\;N\\\\Moment\mathit\;arm\mathit\;\mathit=\mathit\;l\mathit\;\mathit=\mathit\;\mathit1\mathit.\mathit2\mathit\;m\\\\Torque\mathit\;\mathit=\mathit\;\tau\mathit\;\mathit=\mathit\;\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol\tau\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol l\boldsymbol\;\boldsymbol\times\boldsymbol\;\boldsymbol F\\\\\\\tau\mathit\;\mathit=\mathit\;\mathit1\mathit.\mathit2\mathit\;m\mathit\;\mathit\times\mathit\;\mathit{300}\mathit\;N\\\\\tau\mathit\;\mathit=\mathit\;\mathit{360}\mathit\;N\mathit\;m\\\\\boldsymbol T\boldsymbol o\boldsymbol r\boldsymbol q\boldsymbol u\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol i\boldsymbol s\boldsymbol{\mathit\;}\boldsymbol p\boldsymbol o\boldsymbol s\boldsymbol i\boldsymbol t\boldsymbol i\boldsymbol v\boldsymbol e\\\\\\\\\\\\\\\\\\$$
====================================================================================
$$4.5\;\;\;A\;crowbar\;is\;used\;to\\lift\;a\;box\;as\;shown\;in\;the\\figure.\;If\;the\;downward\\force\;of\;250\;N\;is\;applied\\at\;the\;end\;of\;the\;bar,\;how\\much\;weight\;does\;the\\other\;end\;bear\;?\;The\\crowbar\;has\;negligible\;weight.$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Downward\;force\;=\;{\boldsymbol F}_{\mathbf w}\;=\;250\;N\\\\Dis\tan ce\;of\;downward\;force\;=\;d_w\;=\;30\;cm\\\\=\;\frac{30}{100}\;m\;=\;0.3\;m\\\\Required\;weight\;(\;Force\;)\;=\boldsymbol\;\boldsymbol F\;=\;?\\\\Dis\tan ce\;of\;required\;force\;=\;d\;=\;5\;cm\\\\=\;\frac5{100}\;m\;=\;0.05\;m\\\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol\tau}_{\boldsymbol1}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol\tau}_{\boldsymbol2}\boldsymbol{\mathit\;}\\{\boldsymbol d}_{\boldsymbol w}\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}{\boldsymbol F}_{\boldsymbol w}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol d\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol F\boldsymbol{\mathit\;}\\\\\boldsymbol{\mathit(}0.3\;m)\;\times(250\;N)\;=\;(0.05\;m)\;\times\;\boldsymbol F\;\\\\\boldsymbol F\;=\;\frac{\boldsymbol{\mathit(}0.3\;m)\;\times(250\;N)\;}{0.05\;m}\;\\\\\boldsymbol F\;=\;1500\;N\\\\$$
====================================================================================
$$4.6\;\;\;\;A\;\mathit{30}\mathit\;cm\;long\;spanner\\is\;used\;to\;open\;the\;nut\;of\\a\;car.\;If\;the\;torque\;required\\for\;it\;is\;\mathit{150}\mathit\;N\mathit\;m,\;how\;much\\force\;F\;should\;be\;applied\\on\;the\;spanner\;as\;shown\\in\;the\;figure\;below.\\\\\\\\$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\\\Length\;of\;spanner\;=\;l\;=\;30cm\\\\\frac{30\;}{100}\;m\;=\;0.3\;m\\\\Torque\;=\boldsymbol{\mathit\;}\boldsymbol\tau\;=\;150\;N\;m\\\\Force\;=\boldsymbol{\mathit\;}\boldsymbol F\;=\;?\\\\\\\\$$
$$\boldsymbol f\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol\tau\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol F\\\\150\;N\;m\;=\;\;0.3\;m\;\times\;\boldsymbol F\\\\\boldsymbol F\boldsymbol\;=\;\frac{150\;N\;m}{0.3\;m}\boldsymbol\;\\\\\boldsymbol F\;=\;500\;N\\\\\\\\$$
====================================================================================
$$4.9\;\;\;One\;girl\;0f\;30\;kg\\mass\;sits\;1.6\;m\;\;from\\the\;axis\;of\;see\;saw.\\Another\;girl\;of\;mass\\40\;kg\boldsymbol\;wants\;to\;sit\;on\\the\;other\;side,\;so\;that\\the\;see\;saw\;may\;remain\\in\;equilibrium.\;how\;for\\away\;from\;the\;axis,\;the\\other\;girl\;may\;sit\;?\\\\\\\\$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Mass\mathit\;of\mathit\;\mathit1st\mathit\;girl\mathit\;\mathit=\mathit\;m_{\mathit1}\mathit\;\mathit=\mathit\;\mathit{30}\mathit\;kg\\\\Mass\mathit\;of\mathit\;\mathit1st\mathit\;girl\mathit\;\mathit=\mathit\;m_{\mathit2}\mathit\;\mathit=\mathit\;\mathit{40}\mathit\;kg\\\\Dis\mathit{tan}ce\mathit\;of\mathit\;\mathit1st\mathit\;girl\mathit\;from\mathit\;axis\mathit\;\mathit=\mathit\;d_{\mathit1}\mathit\;\mathit=\mathit\;\mathit1\mathit.\mathit6\mathit\;m\\\\Distance\mathit\;of\mathit\;\mathit2nd\mathit\;girl\mathit\;from\mathit\;axis\mathit\;\mathit=\mathit\;d_{\mathit2}\mathit\;\mathit=\mathit\;\mathit?\\\\\\\\$$
$$\boldsymbol C\boldsymbol o\boldsymbol n\boldsymbol d\boldsymbol i\boldsymbol t\boldsymbol i\boldsymbol o\boldsymbol n\boldsymbol{\mathit\;}\boldsymbol f\boldsymbol o\boldsymbol r\boldsymbol{\mathit\;}\boldsymbol e\boldsymbol q\boldsymbol u\boldsymbol i\boldsymbol l\boldsymbol i\boldsymbol b\boldsymbol r\boldsymbol i\boldsymbol u\boldsymbol m\\Clockwise\;moment\;=\;Anticlockwise\;moment\\\\\\\\$$
$${\boldsymbol m}_{\mathbf1}\boldsymbol\;{\boldsymbol d}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol m}_{\mathbf2}\boldsymbol\;{\boldsymbol d}_{\mathbf2}\boldsymbol\;\\(30\;kg\;)\;(1.6\;m)\;=\;(40\;kg)\;d_2\\d_2\;=\;\frac{(30\;kg\;)\;(1.6\;m)}{40\;kg}\\{\boldsymbol d}_{\mathbf2}\;=\;1.2\;m\\Second\;girl\;should\;sit\;1.2\;m\;from\;axis\\\\\\\\$$
====================================================================================
$$4.10\;\;\;\;\;Find\;the\;tension\\in\;each\;string\;as\;shown\\in\;the\;given\;figure,\;if\;the\\block\;weighs\;\;\mathit{150}\mathit\;N.\\\\\\\\$$
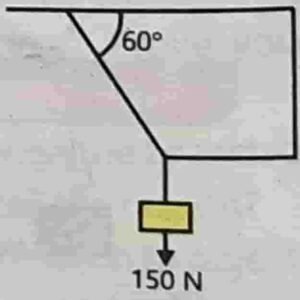
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\;\\weight\;=\;w\;=\;150\;N\\\\Tension\;in\;first\;string\;=\;T_1\;=\;?\\\\Tension\;in\;seconds\;string\;=\;T_2\;=\;?\\\\\\\\$$
After resolving into components.
$$T_1\;\sin\;60\;+\;T_2\;\sin\;0\;=\;150\;N\\\\T_1\;(\frac{\sqrt3}2)\;+\;T_2\;(\;0\;)\;=\;150\;N\\\\T_1\;=\;150\;\times\;\frac2{\sqrt3}\\\\T_1\;=\;\frac{300}{\sqrt3}\;\\\\{\boldsymbol T}_{\boldsymbol1}\;=\;173.2\;N\\\\\\$$
$${\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol c\boldsymbol o\boldsymbol s\boldsymbol\;\mathbf{60}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol T}_{\mathbf2}\boldsymbol\;\boldsymbol c\boldsymbol o\boldsymbol s\boldsymbol\;\mathbf0\\\\(173.20)\;(0.5)\;=\;T_2\;(\;1\;)\\\\{\boldsymbol T}_{\mathbf2}\;=\;86.6\;N\\$$
====================================================================================
Chapter 5
$$\mathit5\mathit.\mathit2\mathit\;\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}A\;body\;moves\;a\\distance\;of\;5\;meters\\in\;a\;straight\;line\;under\\the\;action\;of\;force\;of\\8\;newtons.\;If\;work\\done\;is\;20\;joules,\;find\\the\;angle\;which\;the\;force\\makes\;with\;the\;direction\\of\;motion\;of\;the\;body.\\\\$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Dis\tan ce\;=\;S\;=\;5\;m\\\\Force\;=\;F\;=\;8\;N\\\\work\;done\;=\;W\;=\;20\;J\\\\Angle\;=\;\theta\;=\;?\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol W\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol F\boldsymbol S\boldsymbol{\mathit\;}\boldsymbol c\boldsymbol o\boldsymbol s\boldsymbol{\mathit\;}\boldsymbol\theta$$
$$20\;J\;=\;(\;8\;N\;)\;(\;5\;m\;)\;\cos\;\theta\\\\\frac{20\;J}{\;(\;8\;N\;)\;(\;5\;m\;)\;}\;=\;\;\cos\;\theta\\\\\;\cos\;\theta\;=\;\frac{20\;J}{40\;J}\\\\\cos\;\theta\;=\;\frac12\;J\\\\\theta\;=\;\cos^{-1}\;(\;0.5\;)\\\\\theta\;=\;60\;degree$$
====================================================================================
$$\mathit5\mathit.\mathit5\;\;\;\;A\;ball\;of\;mass\;160\;g\\is\;thrown\;vertically\;upward.\\The\;ball\;reaches\;a\;height\\of\;20\;m.\;Find\;the\;potential\\energy\;gained\;by\;the\;ball\\at\;this\;height.\\\\\\$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol{\mathit\;}\\Mass\;of\;ball\;=\;m\;=\;160\;g\\\\=\;\frac{160}{1000}\;kg\;=\;0.16\;kg\\\\Height\;=\;h\;=\;20\;m\\\\Gravitional\;acceleration\;=\boldsymbol\;\boldsymbol g\boldsymbol\;=\;10\;m\;s^{-2}\\\\Potential\;energy\;=\;P.\;E\;=\;?\\\\\\\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol P\boldsymbol{\mathit.}\boldsymbol{\mathit\;}\boldsymbol E\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol{\mathit\;}\boldsymbol g\boldsymbol{\mathit\;}\boldsymbol h\\\\P.E\;=\;(\;0.16\;kg\;)\;(\;10\;m\;s^{-2}\;)\;(\;20\;m\;)\\\\P.E\;=\;32\;J\;\\\\\\\\$$
====================================================================================
$$\mathit5\mathit.\mathit7\;\;\;\;\;\;\;\;\;A\;girl\;is\;swinging\\on\;a\;swing.\;At\;the\;lowest\\point\;of\;her\;swing,\;she\;is\\1.2\;m\boldsymbol\;from\;the\;ground,\\and\;at\;the\;heighest\;point\\she\;is\;\mathit2\mathit\;m\boldsymbol{\mathit\;}from\;the\;ground.\\What\;is\;her\;maximum\\velocity\;and\;where\;?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Height\;at\;lowest\;point\;=\;h_1\;=\;1.2\;m\\\\Height\;at\;highest\;point\;=\;h_2\;=\;2\;m\\\\Difference\;of\;height\;=\;h_2\;-\;h_1\;\\\\Difference\;of\;height\;=\;2m\;-\;1.2m\;=\;0.8\;m\\\\Maximum\;velocity\;=\;v\;=\;?\\\\\\\\\\\\\\\\\\\\\\\\\\\\$$
$$According\;to\;the\;\boldsymbol l\boldsymbol a\boldsymbol w\boldsymbol{\mathit\;}\boldsymbol o\boldsymbol f\boldsymbol{\mathit\;}\boldsymbol c\boldsymbol o\boldsymbol n\boldsymbol s\boldsymbol e\boldsymbol r\boldsymbol v\boldsymbol a\boldsymbol t\boldsymbol i\boldsymbol o\boldsymbol n\boldsymbol{\mathit\;}\boldsymbol o\boldsymbol f\boldsymbol{\mathit\;}\boldsymbol e\boldsymbol n\boldsymbol e\boldsymbol r\boldsymbol g\boldsymbol y\\\\Potential\;energy\;at\;the\;top\;will\;be\;equal\\to\;the\;kinetic\;energy\;at\;the\;bottom.\\\\\\\\\\\\\\\\\\\\\\\\\\\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol P\boldsymbol{\mathit.}\boldsymbol E\boldsymbol{\mathit\;}\boldsymbol a\boldsymbol t\boldsymbol{\mathit\;}\boldsymbol t\boldsymbol o\boldsymbol p\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol K\boldsymbol{\mathit.}\boldsymbol E\boldsymbol{\mathit\;}\boldsymbol a\boldsymbol t\boldsymbol{\mathit\;}\boldsymbol b\boldsymbol o\boldsymbol t\boldsymbol t\boldsymbol o\boldsymbol m\\\\m\;g\;h\;=\;\frac12\;m\boldsymbol\;\boldsymbol v^{\mathbf2}\;\\\\\;g\;h\;=\;\frac12\boldsymbol\;\boldsymbol\;\boldsymbol v^{\mathbf2}\;\\\\\boldsymbol\;\boldsymbol v^{\mathbf2}\;=\;2\;g\;h\;\\\\\boldsymbol v\;=\;\sqrt{2\;g\;h\;}\;\\\\\boldsymbol v\;=\;\sqrt{2\;(\;10\;m\;s^{-2}\;)\;(\;0.8\;m\;)\;}\;\\\\\boldsymbol v\boldsymbol\;=\;4\;m\;s^{-1}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\$$
$$Maxium\;velocity\;will\;occur\;at\;the\boldsymbol\;\boldsymbol l\boldsymbol o\boldsymbol w\boldsymbol s\boldsymbol t\boldsymbol\;\boldsymbol p\boldsymbol o\boldsymbol i\boldsymbol n\boldsymbol t.\\Because\;at\;lowst\;point\;\boldsymbol P\boldsymbol.\boldsymbol E\;will\;be\boldsymbol\;\boldsymbol z\boldsymbol e\boldsymbol r\boldsymbol o\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\$$
====================================================================================
$$\mathit5\mathit.\mathit8\;\;\;A\;person\;pushes\;a\\lawn\;mover\;with\;a\;force\\of\;50\;N\;making\;an\;angle\\of\;45\;degree\;with\;the\\horizontal.\;If\;the\;mover\\is\;moved\;through\;a\\dis\tan ce\;of\boldsymbol\;20\;m,\;how\\much\boldsymbol\;work\;is\;done\;?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Force\;=\;\boldsymbol F\;=\;50\;N\\\\Angle\;=\;\theta\;=\;45\;degree\\\\Dis\tan ce\;=\;\boldsymbol d\boldsymbol\;=\;20\;m\\\\Work\;=\;W\;=\;\;?\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol W\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol F\boldsymbol d\boldsymbol\;\boldsymbol c\boldsymbol o\boldsymbol s\boldsymbol\;\boldsymbol\theta\\\\W\;=\;(50\;N)\;(20\;m)\;\cos\;45\\\\W\;=\;(1000\;Nm)\;\frac1{\sqrt2}\\\\W\;=\;707.1\;J\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\$$
====================================================================================
$$\mathit5\mathit.\mathit9\;\;\;\;\;\;Calculate\\the\;work\;done\;in\\(i)\;\;pushing\;a\boldsymbol\;5\;kg\\box\;up\;a\;frictionless\\inclined\;plane\;10\;m\\long\;that\;makes\;an\\angle\;of\;30\;degree\\with\;the\;horizontal.\\(ii)\;\;Lifting\;the\;box\\vertically\;up\;from\;the\\ground\;to\;the\;top\;of\\the\;inclined\;plane.$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;=\;m\;=\;5\;kg\\\\Dis\tan ce\;=\;d\;=\;10\;m\\\\Angle\;=\;\theta\;=\;30\;degree\\\\Work\;done\;=\;W\;=\;?\\$$
$$Gravity\;acts\;downward\\\boldsymbol F\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol w}_{\mathbf y}\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol m\boldsymbol\;\boldsymbol g\boldsymbol\;\mathbf{sin}\boldsymbol\;\boldsymbol\theta\\\\\boldsymbol F\;=\;(\;5\;kg\;)\;(\;10\;m\;s^{-2}\;)\;sin\;30\\\\\boldsymbol F\;=\;(\;50\;kg\;m\;s^{-2})\;(\;0.5\;)\\\\\boldsymbol F\boldsymbol\;=\;25\;N\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol W\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol F\boldsymbol{\mathit\;}\boldsymbol d\\\\W\;=(\;25\;N\;)\;(\;10\;m\;)\\\\W\mathit\;\mathit=\mathit\;\mathit{250}\mathit\;J\\\\$$
$$\boldsymbol S\boldsymbol i\boldsymbol n\boldsymbol\;\mathbf{30}\boldsymbol\;\boldsymbol=\boldsymbol\;\frac{\mathbf P\mathbf e\mathbf r\mathbf p\mathbf e\mathbf n\mathbf d\mathbf i\mathbf c\mathbf u\mathbf l\mathbf a\mathbf r}{\mathbf H\mathbf y\mathbf p\mathbf o\mathbf t\mathbf e\mathbf n\mathbf u\mathbf s\mathbf e}\\\\\\\frac12\;=\;\frac h{10\;m}\\\\\frac{10\;m}2\;=\;h\\\\h\;=\;5\;m\\\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol W\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol{\mathit\;}\boldsymbol g\boldsymbol{\mathit\;}\boldsymbol h\\\\W\;=\;(\;5\;k\;g\;)\;(\;10\;m\;s^{-2}\;)\;(\;5\;m\;)\\\\W\;=\;250\;J\\\\$$
====================================================================================
$$\mathit5\mathit.\mathit{12}\;\;\;\;A\;\;40\;kg\;boy\\runs\;up-stair\;\;10\;m\\high\;in\;8\;s.\;What\\power\;he\;developed\;\\\\$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;=\;m\;=\;40\;kg\\\\Height\;=\;h\;=\;10\;m\\\\Time\;=\;s\;=\;8\;s\\\\Power\;=\;P\;=\;?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol w\boldsymbol o\boldsymbol r\boldsymbol k\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol P\boldsymbol o\boldsymbol t\boldsymbol e\boldsymbol n\boldsymbol t\boldsymbol i\boldsymbol a\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol e\boldsymbol n\boldsymbol e\boldsymbol r\boldsymbol g\boldsymbol y\\\boldsymbol W\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol P\boldsymbol{\mathit.}\boldsymbol E\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol{\mathit\;}\boldsymbol g\boldsymbol{\mathit\;}\boldsymbol h\\\\W\;=\;(\;40\;kg\;)\;(\;10\;m\;s^{-2}\;)\;(\;10\;m\;)\\\\W=\;4000\;J\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol P\boldsymbol o\boldsymbol w\boldsymbol e\boldsymbol r\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol W\boldsymbol o\boldsymbol r\boldsymbol k}{\boldsymbol t\boldsymbol i\boldsymbol m\boldsymbol e}\boldsymbol{\mathit\;}\\\boldsymbol P\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol W}{\boldsymbol t}\\\\P\;=\;\frac{4000\;J}{8\;s}\\\\P\;=\;500\;W\\\\$$
====================================================================================
$$\mathit5\mathit.\mathit{13}\;\;\;\;\;\;A\;force\;acts\\through\;a\;dis\tan ce\boldsymbol\;L\\on\;a\;body.\;The\;force\\is\;then\;increased\;to\\2F\;\;that\;further\;acts\\through\;\;2L.\;\;Sketch\\a\boldsymbol\;force-displacement\\graph\boldsymbol\;and\;calculate\;the\\total\;workdone.$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Initial\;force\;=\;F_1\;=\;F\\Increased\;force\;=\;F_2\;=\;2F\\Initial\;dis\tan ce\;=\;d_1\;=\;L\\Further\;dis\tan ce\;=\;d_2\;=\;2L\\Total\;Work\;done\;=\;W\;=\;?$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol W\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol F\boldsymbol{\mathit\;}\boldsymbol d\\\\Initial\;Work\;done\;=\;W_1\;=\;F_1\;d_1\;=\;F\;L\\\\Further\;Work\;done\;=\;W_2\;=\;F_2\;d_2\\\\=\;(\;2F\;)\;(\;2L\;)\;=\;4\;F\;L\\\\Total\;Work\;done\;=\;W\;=\;W_1\;+\;W_2\;\\So\\\\W\;=\;F\;L\;+\;4\;F\;L\;=\;5\;F\;L$$
Chapter 6
$$6.3\;\;\;\;\;When\;a\;solid\;of\\mass\;60\;g\;is\;lowered\\into\;a\;measuring\;cylinder,\\the\;level\;of\;water\;rises\\from\;\;40\;c\;m^3\;to\;44\;c\;m^3.\\Calculate\;the\;density\;of\\the\;solid.$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;=\;m\;=\;60\;g\;=\;\frac{60}{1000}\;kg\;=\;0.06\;kg\\\\Initial\;level\;of\;water\;=\;V_1\;=\;40\;c\;m^3\;\\\\=\;\frac{40}{1000000}\;m^3\;=0.000040\;m^3\;\\\\Final\;level\;of\;water\;=\;V_2\;=\;44\;c\;m^3\;\\\\=\;\frac{44}{1000000}\;m^3\;=0.000044\;m^3\;\\\\Volume\;=\;V\;=Final\;level\;-\;initial\;level\\\\=\;0.000044\;m^3\;-\;0.000040\;m^3\\\\=0.000004\;m^3\;\\\\Density\;=\;\rho\;=\;?\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol D\boldsymbol e\boldsymbol n\boldsymbol s\boldsymbol i\boldsymbol t\boldsymbol y\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol m\boldsymbol a\boldsymbol s\boldsymbol s}{\boldsymbol v\boldsymbol o\boldsymbol l\boldsymbol u\boldsymbol m\boldsymbol e}\\\boldsymbol\rho\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{\boldsymbol m}{\boldsymbol V}\\\\\rho\;=\;\frac{0.06\;kg}{0.000004\;m^3}\;\\\\\rho\;=\;15000\;kg\;m^{-3}\\\\\rho\;=\;15\;\times\;10^3\;kg\;m^{-3}\\$$
==========================================
$$\mathit6\mathit.\mathit8\;\;\;Find\;the\;water\;pressure\\on\;a\;deep-sea\;diver\;at\;a\\depth\;of\;10\;m,\;where\;the\\density\;of\;sea\;water\;is\\1030\;kg\;m^{-3}\\\\$$
$$Depth\;=\;h\;=\;10\;m\\Density\;of\;sea\;water\;=\;\rho\;=\;1030\;kg\;m^{-3}\\Gravitional\;acceleration\;=\;g\;=\;10\;m\;s^{-2}\\Pressure\;=\;P\;=\;?\\\\P\mathit\;\mathit=\mathit\;\rho\mathit\;g\mathit\;h\;\\\\P\;=\;(1030\;kg\;m^{-3}\;)\;(\;10\;m\;s^{-2}\;)\;(\;10\;m\;)\\P\;=\;103000\;kg\;m\;s^{-2}\;m^{-2}\\P\;=\;1.03\;\times\;10^5\;N\;m^{-2}\;\\P\;=\;1.03\;\times\;10^5\;Pa$$
==========================================
$$\mathit6\mathit.\mathit{10}\;\;\;In\;a\;hot\;air\;balloon,\;the\\following\;data\;was\;recorded.\\Draw\;a\;graph\;between\;the\\altitude\;and\;pressure\;and\\find\;out:\\(a)\;What\;would\;the\boldsymbol\;air\\pressure\;have\;been\\at\;sea\;level\;?\\(b)\;At\;what\;height\;the\;air\\pressure\;would\;have\;been\\90\;kPa\;?\\Altitude\;(m)\boldsymbol:\;\;150,\;500,\\800,\;1140,\;1300,\;1500\\Pressure\;(kPa)\boldsymbol:\;99.5,\;95.7,\\92.4,\;88.9,\;87.2,\;85.3$$
$$Pressure\;=\;P\\Slope\;=\;m\\Altitude\;=\;h\\Y\;intercept\;=\;c\\\\Lets\;first\;slove\;the\;question\;with\;the\\help\;of\;slope\;intercept\;form\\\\P\;=\;m\;h\;+\;c\\P\;=\;-\;0.00939\;h\;+\;100.99\\P\;=\;101000\;Pa\\\\P\;=\;m\;h\;+\;c\\90\;=\;-\;0.00939\;h\;+\;100.99\\h\;=\;1040.38\;m$$
==========================================
$$6.11\;\;\;\;\;\;\;If\;the\;pressure\;in\;a\\hydraculic\;press\;is\;increased\\by\;an\;additional\;10\;N\;c\;m^{-2},\\how\;much\;extra\;load\;will\;the\\output\;platform\;support\;if\\its\;cross-sectional\;area\\is\boldsymbol\;50\;c\;m^2.$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Additional\;pressure\;=\;P\;=\;10\;N\;c\;m^{-2}\\=\;10^5\;N\;m^{-2}\\\\Area\;=\;A\;=\;\boldsymbol\;50\;c\;m^2\;=\;50\;\times\;10^{-4}\;m^2\\Load\;=\;F\;=\;?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol P\boldsymbol\;\boldsymbol=\boldsymbol\;\frac{\mathbf F}{\mathbf A}\\\\F\;=\;P\;A\\\\F\;=\;(\;\;10^5\;N\;m^{-2}\;)\;(\;50\;\times\;10^{-4}\;m^2\;)\\\\F\;=\;500\;N$$
==========================================
$$\mathit6\mathit.\mathit{12}\;\;The\;force\;exerted\\normally\;on\;the\;hydraulic\\brake\;system\;of\;a\;car,\\with\;its\;piston\;of\;cross\\sectional\boldsymbol\;area\;5\;c\;m^2\\is\;500\;N.\;What\;will\;be\;the:\\(a)\;\;pressure\;transferred\\to\;the\;brake\;oil\;?\\(b)\;\boldsymbol\;force\;on\;the\;brake\\piston\;of\;area\boldsymbol\;of\\cross\;section\;20\;c\;m^2$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Force\;on\;1st\;piston\;=\;F_1\;=\;500\;N\\\\Area\;of\;1st\;piston\;=\;A_1\;=\;\;5\;c\;m^2\\=\;\frac5{10000}\;m^2\;=\;0.0005\;m^2\\\\Area\;of\;2nd\;piston\;=\;A_2\;=\;\;20\;c\;m^2\\=\;\frac{20}{10000}\;m^2\;=\;0.002\;m^2\\\\Pressure\;=\;P\;=?\\\\Force\;on\;2nd\;piston\;=\;F_2\;=\;?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol P\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{{\boldsymbol F}_{\boldsymbol1}}{{\boldsymbol A}_{\boldsymbol1}}\\\\P\;=\;\frac{500\;N}{0.0005\;m^2}\\\\P\;=\;10^6\;N\;m^2\\\\\boldsymbol P\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\frac{{\boldsymbol F}_{\boldsymbol2}}{{\boldsymbol A}_{\boldsymbol2}}\\\\F_2\;=\;P\;A_2\\\\F_2\;=\;(\;10^6\;N\;m^2\;)\;(\;0.002\;m^2\;)\\\\F_2\;=\;2000\;N\\$$
====================================================================================
Chapter 7
$$7.5\;\;The\;ice\;and\;steam\\points\;on\;a\;ungraduated\\therometer\;are\;found\;to\\be\;192\;mm\;apart.\;What\\temperature\;will\;be\;on\\Celsius\;scale\;if\;the\;length\\of\;mercury\;thread\;is\;at\\67.2\;mm\boldsymbol\;above\;the\\ice\;point\;mark\;?$$
$$\boldsymbol A\boldsymbol{\mathit\;}\boldsymbol t\boldsymbol h\boldsymbol e\boldsymbol r\boldsymbol m\boldsymbol o\boldsymbol m\boldsymbol e\boldsymbol t\boldsymbol e\boldsymbol r\boldsymbol{\mathit\;}\boldsymbol w\boldsymbol i\boldsymbol t\boldsymbol h\boldsymbol{\mathit\;}\boldsymbol n\boldsymbol o\boldsymbol{\mathit\;}\boldsymbol s\boldsymbol c\boldsymbol a\boldsymbol l\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol i\boldsymbol s\\\boldsymbol c\boldsymbol a\boldsymbol l\boldsymbol l\boldsymbol e\boldsymbol d\boldsymbol{\mathit\;}\boldsymbol u\boldsymbol n\boldsymbol g\boldsymbol r\boldsymbol a\boldsymbol d\boldsymbol u\boldsymbol a\boldsymbol t\boldsymbol e\boldsymbol d\boldsymbol{\mathit\;}\boldsymbol t\boldsymbol h\boldsymbol e\boldsymbol r\boldsymbol m\boldsymbol o\boldsymbol m\boldsymbol e\boldsymbol t\boldsymbol e\boldsymbol r$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Length\;between\;ice\;point\;and\;steam\;point=192mm\\\\Ice\;point\;=\;0\;degree\;Celsius\\\\Steam\;point\;=\;100\;degree\;Celsius\\\;\\Temperature\;on\;Celsius\;scale\;=\;T_c$$
$$Length\;of\;mercury\;=\;67.2\;mm\\$$
$$\boldsymbol S\boldsymbol o\boldsymbol l\boldsymbol u\boldsymbol t\boldsymbol i\boldsymbol o\boldsymbol n\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\Temperature\;rise\;per\;mm=\;\frac{100^\circ\;C\;-\;0^\circ C}{Dis\tan ce\;apart}\\\\Temperature\;rise\;per\;mm=\;\frac{100^\circ\;C\;-\;0^\circ C}{192mm}\\\\Temperature\;rise\;per\;mm=\;0.52^\circ\;C\;per\;mm$$
$$Hence\\\\T_c\;=\;0.52^\circ\;C\;per\;mm\;\times\;67.2\;mm\\\\T_c\;=\;34.9^\circ\;C\;per\;mm\;\times\;1\;mm\\\\T_c\;=\;35^\circ\;C\\$$
==========================================
$$\mathit7\mathit.\mathit6\;\;The\;length\;between\\the\;fixed\;point\;of\\liquid-in-glass\\thermometer\;is\;20cm.\\If\;the\;mercury\;level\;is\\4.5\;cm\;above\;the\;lower\\mark,\;what\;is\;the\\temperature\;on\;the\\Fahrenheit\;scale?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Length\;between\;fixed\;point\;=\;20cm\\\\Mercury\;level\;above\;lower\;fixed\;point\;=\;4.5cm\\\\Temperature\;in\;Fahrenheit\;=\;T_f\;=\;?$$
$$\boldsymbol S\boldsymbol o\boldsymbol l\boldsymbol u\boldsymbol t\boldsymbol i\boldsymbol o\boldsymbol n\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\Lower\;fixed\;point\;=\;0cm\;=\;32^\circ F\\\\Upper\;fixed\;point\;=\;20cm\;=\;212^\circ F\\\\20cm-0cm\;=\;212^\circ F-32^\circ F\\\\20\;cm\;=\;180^\circ F\\\\1\;cm\;=\;\frac{180^\circ F}{20}\\\\1\;cm\;=\;9^\circ F\\\\$$
$$Mercury\;is\;at\;4.5\;cm,starting\;from\;32^\circ F\\\\So\\Temperature\;above\;32^\circ F\;=\;9\times4.5cm\\\\Temperature\;above\;32^\circ F\;=\;40.5^\circ F\\\\Hence\\\\T_f\;=\;40.5^\circ F\;+\;32^\circ F\;=\;72.5^\circ F\\\\\\$$
====================================================================================
Check! Some important links below
Revised Syllabus 9th Class Physics Short Questions
Revised Syllabus 9th Class Physics Chapter 1 video




