Physics Class 9 New Book Chapter 4 Solved Exercise
Physics Class 9 New Book Chapter 4 Solved Exercise
9th Class Physics New Book 2025 Chapter 4 MCQs
4.1 A particle is simultaneously acted upon by two forces of 4 and 3 newtons. The net force particle is:
(a) 1 N (b) between 1 N and 7 N (c) 5N (d) 7 N
Option (b) is correct.
Explanation:-
If the the forces are in same direction their sum will be 7 N and id they are in opposite direction their sum will ne 1N.
====================================================================================
4.2 A force F is making an angle of 60 degree with x-axis. Its y-component is equal to:
(a) F (b) F Sin60 (c) F Cos60 (d) F Tan60
Option (b) is correct.
Explanation:-
X-component will be F Cos 60 and Y-component will be F Sin 60.
====================================================================================
4.3 Moment of force is called:
(a) moment arm (b) couple (c) couple arm (d) torque
Option (d) is correct.
Explanation:-
Another name of torque is moment.
====================================================================================
4.7 In stable equilibrium, the centre of gravity of the body lies:
(a) at the highest position (b) at the lowest position
(c) at any position (d) outside the body
Option (b) is correct.
Explanation:-
Centre of gravity is at lowest position because small tilt rises the centre of gravity and gravity pulls it back down to balance again.
====================================================================================
4.9 A cylinder resting on its circular base is in:
(a) stable equilibrium (b) unstable equilibrium
(c) neutral equilibrium (d) none of these
Option (a) is correct.
Explanation:-
A cylinder resting on its circular base in in stable equilibrium because when it is slightly tilted, it comes back to its original position.
====================================================================================
4.10 Centripetal force is given by:
$$(a)\;r\;F\\(b)\;r\;F\;Cos\;Ɵ\\(c)\;\frac{m\;v^2}r\\(d)\;\frac{m\;v}{r^2}$$
Option (c) is correct.
Explanation:-
$$Centripetal\;acceleration\\is\;equal\;to\;\;\frac{v^2}r\\We\;know\;that\\F=\;m\;a\\Hence\\F\;=\;m\;\frac{v^2}r\\F=\;\frac{m\;v^2}r$$
9th physics New Book Chapter4 Short Question Answer
4.1 Define like and unlike parallel forces.
We call parallel forces acting in same direction ” like parallel forces ” and those acting in opposite direction ” unlike parallel forces’.
====================================================================================
4.2 What are rectangular components of a vector and their values?
We resolve a force into two components that are perpendicular to each other. We call these components as perpendicular or rectangular components of the force.
$$Horizontol\;component\\is\;represented\;by\;F_x$$ $$F_x=F\;Cos\theta$$
$$Vertical\;component\\is\;represented\;by\;F_y$$ $$F_y=F\;Sin\theta$$
====================================================================================
4.3 What is the line of action of a force?
The line along which the force acts is called the line of action of the force.
====================================================================================
4.4 Define moment of a force. Prove that
$$\tau\;=\;rF\;Sin\theta$$ where Ɵ is angle between r and F.
Moment of the force or torque is defined as the product of the force and the moment arm.
Let a force F is applied on an object at point P which is at a distance r from the origin.
$$Angle\;between\;r\;and\;F\;is\;\theta.\\Horizontal\;and\;vertical\\components\;of\;force\;F\\are\;F\;Cos\theta\;and\;F\;Sin\theta\\respectively.$$
There will be rotation only due to vertical component of force and no rotation due to horizontal component of the force because the line of action of horizontal component of force will pass through the origin.
We call perpendicular distance from the line of action of force to the origin the moment arm, denoted by r.
$$Torque=Moment\;arm\times force\\\tau\;=\;r\;F_y\\\tau\;=\;r\;F\;S\mathrm{in}\theta\;\\$$
====================================================================================
4.7 Give an example of the body which is moving yet in equilibrium.
A car which is moving on a straight road at constant speed is in dynamic equilibrium.
====================================================================================
9th Physics Chapter 4 Constructed Response Questions
9th Physics New Chapter 4 Constructed Response Questions
4.1 A car travels at the same speed around two curves with different radii. For which radius the car experience more centripetal force? Prove your answer.
If same car travels with same speed around two curves with different radii, for smaller radius car will experience greater centripetal force. Because mass and speed will be constant and radius of the circle will be inversely proportional to the centripetal force.
$$F\;=\;\frac{m\;v^2}r\\If\;m\;and\;v\;are\;cons\tan t\\then\\F\;\propto\frac1r$$
=========================================
4.2 A ripe mango does not normally fall from the tree. But when the branch of the tree is shaken, the mango falls down easily. Can you tell the reason?
It happens due to inertia. When branch moves, mango want to stay in its original state due to inertia. Due to this, stem of the mangoes experiences a force and the mango falls down. This is an example of Newton’s first law of motion.
=========================================
4.4 Why an accelerated body cannot be considered in equilibrium?
An accelerated body cannot be considered in equilibrium because acceleration means forces are unbalanced.
A body is said to be in equilibrium if all the forces acting on it are balanced and its state of motion does not change
=========================================
9th Physics Chapter 4 long questions
9th Physics Chapter 4 long questions.
4.1 Explain the principle of moments with an example.
Principles of moments states that when a body is in balanced position, the sum of clockwise moments about any point equals the sum of anticlockwise moments about that point.
A child weighing 200 Newton sits 2 meter from the pivot on the left side. Another child sits on the right side at a distance of 4 meter from the pivot.
Anticlockwise moment = 200 x 2 = 400 Nm
So, the force on the right side is
F x 4 = 400
F = 100
Hence a child of 100 N sitting 4 m away balances the seesaw.
============
4.3 State and explain two conditions of equilibrium.
First condition of equilibrium
A body is said to be in translational equilibrium only if the vector of sum of all the external forces acting on it is equal to zero.
By Newton’s second law of motion, F=ma if the body is in translational equilibrium, the a=0, therefore net force should be zero.
Mathematical form:-
$${\textstyle\sum_{}}F=0\\or\\{\textstyle\sum_{}}{\textstyle{\scriptstyle F}_x}{\textstyle=}{\textstyle0}{\textstyle\;}{\textstyle a}{\textstyle n}{\textstyle d}{\textstyle\;}{\textstyle\sum_{}}{\textstyle{\scriptstyle F}_y}{\textstyle=}{\textstyle0}$$
============
Second condition of equilibrium
The vector sum of all the torques acting on a body about any point must be zero.
It implies to rotational equilibrium which means that the body should not rotate under the action of the forces.
If first condition is satisfied, the system may still not be in complete equilibrium.. If the forces are forming a couple, they will rotate the object.. Hence for complete equilibrium both the conditions must satisfy.
Mathematical form:-
$${\textstyle\sum_{}}\tau=0$$
Hence for complete equilibrium
$$\textstyle\sum_{}F_x=0\;and\\\sum_{}F_y=0\;and\\\sum_{}\tau==0$$
============
9th Physics New Book Chapter 4 Numerical
$$4.1\boldsymbol{\mathit\;}\;\;A\;force\;of\;200\;N\;is\\acting\;on\;a\;cart\;at\;an\\angle\;of\;30\;degree\;with\\the\;horizontal\;direction.\\Find\;x\;and\;y\;components\\of\;the\;force\\\\\\\\$$
$$Data:-\\Force\;=\;F\;=\;200\;N\\Angle\;=\;\theta\;=\;30\;degree\\Horizontal\;component\;=\;F_x\;=\;?\\Vertical\;\;component\;=\;F_y\;=\;?\\$$
$$\\Formula:-\\F_{\mathrm x}\;=\;F\;cos\;\theta\\\\\\F_x\mathit\;\mathit=\mathit\;\mathit(\mathit{200}\mathit\;N\mathit)\mathit\;cos\mathit\;\mathit{30}\\\\F_x\mathit\;\mathit=\mathit\;\mathit(\mathit{200}\mathit\;N\mathit)\mathit\;\mathit\times\mathit\;\frac{\sqrt{\mathit3}}{\mathit2}\mathit\;\\\\F_x\mathit\;\mathit=\mathit\;\mathit(\mathit{100}\mathit\;N\mathit)\mathit\;\mathit\times\mathit\;\sqrt{\mathit3}\mathit\;\\\\F_x\mathit\;\mathit=\mathit\;\mathit(\mathit{100}\mathit\;N\mathit)\mathit\times\mathit1\mathit.\mathit{732}\\\\F_x\mathit\;\mathit=\mathit\;\mathit{173}\mathit.\mathit2\mathit\;N\\\\\\Formula:-\\F_{\mathrm y}\;=\;F\;sin\;\theta\\\\\\F_y\mathit\;\mathit=\mathit\;\mathit(\mathit{200}\mathit\;N\mathit)\mathit\;sin\mathit\;\mathit{30}\\\\F_y\mathit\;\mathit=\mathit\;\mathit(\mathit{200}\mathit\;N\mathit)\mathit\;\mathit\times\mathit\;\frac{\mathit1}{\mathit2}\mathit\;\\\\F_y\mathit\;\mathit=\mathit\;\mathit{100}\mathit\;N$$
====================================================================================
$$4.3\;\;\;\;\;\;\;Two\;weights\;are\\hanging\;from\;a\;meter\;rule\\at\;the\;positions\;as\;shown\\in\;the\;figure.\;If\;the\;meter\\rule\;is\;balanced\;at\;its\\centre\;of\;gravity\;(C.G),\;find\\the\;unknown\;weight\;w.$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\w_1\;=\;4\;N\\\\d_1\;=30\;cm\;=\;\frac{30}{100}m\;=\;0.3\;m\\\\d_2\;=40\;cm\;=\;\frac{40}{100}m\;=\;0.4\;m\\\\w\;=\;?\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol w}_{\boldsymbol1}\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}{\boldsymbol d}_{\boldsymbol1}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol w\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}{\boldsymbol d}_{\boldsymbol2}\;\\\\4\;N\;\times\;0.3\;m\;=\;w\;\times\;0.4\;m\\\\w\;=\;\frac{4\;N\;\times\;0.3\;m}{0.4\;m}\\\\w\;=\;3\;N\\\\\\$$
====================================================================================
$$4.4\;\;\;A\;sea-saw\;is\;balanced\\with\;two\;children\;sitting\;near\\either\;end.\;Child\;A\;weighs\\30\;kg\;and\;sits\;2\;metres\;away\\from\;the\;pivot,\;while\;child\;B\\weighs\;40\;kg\;and\;sits\;1.5\\metres\;from\;the\;piovt.\\Calculate\;the\;total\;moment\\on\;each\;side\;and\;determine\\if\;sea-saw\;is\;in\;eqilibrium.$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;of\;chlid\;A\;=\;m_1\;=\;30\;kg\\\\Mass\;of\;chlid\;B\;=\;m_1\;=\;40\;kg\\\\Dis\tan ce\;of\;child\;A\;from\;pivot\;=l_1\;=\;2\;m\\\\Dis\tan ce\;of\;child\;B\;from\;pivot\;=l_2\;=\;1.5\;m\\\\Moment\;of\;child\;A\;=\;\tau_1\;=\;?\\\\Moment\;of\;child\;A\;=\;\tau_2\;=\;?\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\\boldsymbol T\boldsymbol o\boldsymbol r\boldsymbol q\boldsymbol u\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol\tau\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol F\\\boldsymbol T\boldsymbol o\boldsymbol r\boldsymbol q\boldsymbol u\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol\tau\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol W\\\boldsymbol T\boldsymbol o\boldsymbol r\boldsymbol q\boldsymbol u\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol\tau\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol g\\\\Moment\;of\;child\;A\;=\boldsymbol\;{\boldsymbol\tau}_{\mathbf1}\;=\;l_1\;\times\;F_1\\\\=\;l_1\times w_1=l_1\;\times\;m_1\;g=(2\;m)\times(30\;kg)(10\;m\;s^{-2})\\\\=\;(2\;m)\times(300\;kg\;m\;s^{-2})\;=\;600\;Nm\\\\\\Moment\;of\;child\;B\;=\;{\boldsymbol\tau}_{\mathbf2}\;=\;l_2\;\times\;F_2\\\\=\;l_2\times w_2=l_2\;\times\;m_2\;g=(1.5m)\times(40\;kg)(10\;m\;s^{-2})\\\\=\;(1.5\;m)\times(400\;kg\;m\;s^{-2})\;=\;600\;Nm\\\\\\\;Since\;\boldsymbol{\mathit\;}{\boldsymbol\tau}_{\boldsymbol1\boldsymbol{\mathit\;}}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol\tau}_{\boldsymbol2\boldsymbol{\mathit\;}}\\Therefore\;system\;is\;in\;equilibrium.\\$$
====================================================================================
$$4.7\;\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}A\;5\;N\;ball\;hanging\\from\;a\;rope\;is\;pulled\;to\\the\;right\;by\;a\;horizontal\\force\;F.\;This\;rope\;makes\\an\;angle\;of\;60^\circ\;with\;the\\ceiling,\;as\;shown\;in\;the\\given\;figure.\;Determine\\the\;magnitude\;of\;force\;F\\and\;tension\;T\;in\;the\;string.\\\\\\\\$$
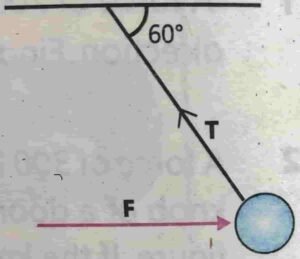
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\\\Weight\;of\;ball\;=\boldsymbol\;\boldsymbol w\;=?\;\\\\Angle\;=\;\theta\;=\;60\;degree\\\\Force\;=\;\boldsymbol F\;=?\\\\Tension\;=\;T\;=?\\\\\\\\\\$$
$$\boldsymbol F\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol w\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf5\boldsymbol\;\boldsymbol N\\\\\boldsymbol V\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol i\boldsymbol c\boldsymbol a\boldsymbol l\boldsymbol l\boldsymbol y\\\\T_y\;=\;w\\\\\boldsymbol T\boldsymbol\;\boldsymbol s\boldsymbol i\boldsymbol n\boldsymbol\;\boldsymbol\theta\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol w\\\\\boldsymbol T\;\sin\;60\;=\;5\;N\\\\\boldsymbol T\;(\frac{\sqrt3}2)\;=\;5\;N\\\\\boldsymbol T\;=\;\frac{5\;N}{\frac{\sqrt3}2}\\\\\boldsymbol T\;=\;\frac{10}{\sqrt3}N\\\\\boldsymbol T\boldsymbol\;=\;5.77\;N\\\\\\\boldsymbol H\boldsymbol o\boldsymbol r\boldsymbol i\boldsymbol z\boldsymbol o\boldsymbol n\boldsymbol t\boldsymbol a\boldsymbol l\boldsymbol l\boldsymbol y\boldsymbol\;\\\\\\\boldsymbol F\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol T\boldsymbol\;\boldsymbol c\boldsymbol o\boldsymbol s\boldsymbol\;\boldsymbol\theta\\\\\boldsymbol F\;=\;5.77\;N\;\times\;0.5\;\\\\\boldsymbol F\;=\;2.89\;N\\\\\\\\\\\\$$
====================================================================================
$$4.8\;\;\;A\;sign\;board\;is\\suspended\;by\;mans\\of\;two\;steel\;wires\;as\\shown\;in\;the\;given\;figure.\\If\;the\;weight\;of\;the\;board\\is\;200\;N,\;what\;is\;the\\tension\;in\;the\;strings\;?$$
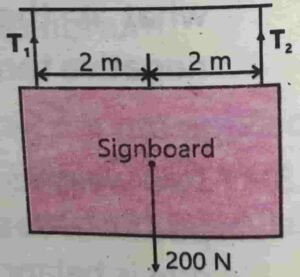
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\weight\;=\;w\;=\;200\;N\\\\Tension\;is\;1st\;string\;=\;T_1\;=\;?\\\\Tension\;is\;2nd\;string\;=\;T_2\;=\;?$$
$$Vertical\;forces\;will\;balance\;each\;other\\\\{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol+\boldsymbol\;{\boldsymbol T}_{\mathbf2}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{200}\boldsymbol\;\boldsymbol N\\\\Wires\;are\;symmetrically\;placed.\\\\Hence\;\\\\{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol T}_{\mathbf2}\boldsymbol\;\\\\So\\{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol+\boldsymbol\;{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{200}\boldsymbol\;\boldsymbol N\\\\2{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol\;=\;200\;N\\\\{\boldsymbol T}_{\mathbf1}\;=\;\frac{\;200\;N}2\\\\{\boldsymbol T}_{\mathbf1}\;=\;100\;N\\\\But\\{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol T}_{\mathbf2}\\\\So\;\\\\{\boldsymbol T}_{\mathbf2}\;=\;100\;N\\\\\\\\$$
$$Hence\;tension\;in\;each\;string\;in\;\boldsymbol{100}\boldsymbol{\mathit\;}\boldsymbol N\\\\\\\\$$
====================================================================================
9th Class Physics Short Questions Chapter 4
9th Class Physics New Book 2025 Solved Exercise Chapter 3
Home Page Notespunjab.com



