9th Physics New Book Chapter 4 Numerical
Solution of Numerical chapter 4 Class 9th New Physics Book 2025
$$4.1\boldsymbol{\mathit\;}\;\;A\;force\;of\;200\;N\;is\\acting\;on\;a\;cart\;at\;an\\angle\;of\;30\;degree\;with\\the\;horizontal\;direction.\\Find\;x\;and\;y\;components\\of\;the\;force\\\\\\\\$$
$$Data:-\\Force\;=\;F\;=\;200\;N\\Angle\;=\;\theta\;=\;30\;degree\\Horizontal\;component\;=\;F_x\;=\;?\\Vertical\;\;component\;=\;F_y\;=\;?\\$$
$$\\Formula:-\\F_{\mathrm x}\;=\;F\;cos\;\theta\\\\\\F_x\mathit\;\mathit=\mathit\;\mathit(\mathit{200}\mathit\;N\mathit)\mathit\;cos\mathit\;\mathit{30}\\\\F_x\mathit\;\mathit=\mathit\;\mathit(\mathit{200}\mathit\;N\mathit)\mathit\;\mathit\times\mathit\;\frac{\sqrt{\mathit3}}{\mathit2}\mathit\;\\\\F_x\mathit\;\mathit=\mathit\;\mathit(\mathit{100}\mathit\;N\mathit)\mathit\;\mathit\times\mathit\;\sqrt{\mathit3}\mathit\;\\\\F_x\mathit\;\mathit=\mathit\;\mathit(\mathit{100}\mathit\;N\mathit)\mathit\times\mathit1\mathit.\mathit{732}\\\\F_x\mathit\;\mathit=\mathit\;\mathit{173}\mathit.\mathit2\mathit\;N\\\\\\Formula:-\\F_{\mathrm y}\;=\;F\;sin\;\theta\\\\\\F_y\mathit\;\mathit=\mathit\;\mathit(\mathit{200}\mathit\;N\mathit)\mathit\;sin\mathit\;\mathit{30}\\\\F_y\mathit\;\mathit=\mathit\;\mathit(\mathit{200}\mathit\;N\mathit)\mathit\;\mathit\times\mathit\;\frac{\mathit1}{\mathit2}\mathit\;\\\\F_y\mathit\;\mathit=\mathit\;\mathit{100}\mathit\;N$$
====================================================================================
$$4.2\;\;\;A\;force\;of\;300\;N\;is\\applied\;perpendicularly\;at\\the\;knob\;of\;a\;door\;to\;open\\it.\;If\;knob\;is\;1.2\;m\;away\\from\;the\;hinge,\;what\;is\;the\\torque\;applied\;?\;Is\;it\\positive\;or\;negative\;torque?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Force\mathit\;\mathit=\mathit\;F\mathit\;\mathit=\mathit\;\mathit{300}\mathit\;N\\\\Moment\mathit\;arm\mathit\;\mathit=\mathit\;l\mathit\;\mathit=\mathit\;\mathit1\mathit.\mathit2\mathit\;m\\\\Torque\mathit\;\mathit=\mathit\;\tau\mathit\;\mathit=\mathit\;\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol\tau\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol l\boldsymbol\;\boldsymbol\times\boldsymbol\;\boldsymbol F\\\\\\\tau\mathit\;\mathit=\mathit\;\mathit1\mathit.\mathit2\mathit\;m\mathit\;\mathit\times\mathit\;\mathit{300}\mathit\;N\\\\\tau\mathit\;\mathit=\mathit\;\mathit{360}\mathit\;N\mathit\;m\\\\\boldsymbol T\boldsymbol o\boldsymbol r\boldsymbol q\boldsymbol u\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol i\boldsymbol s\boldsymbol{\mathit\;}\boldsymbol p\boldsymbol o\boldsymbol s\boldsymbol i\boldsymbol t\boldsymbol i\boldsymbol v\boldsymbol e\\\\\\\\\\\\\\\\\\$$
====================================================================================
$$4.3\;\;\;\;\;\;\;Two\;weights\;are\\hanging\;from\;a\;meter\;rule\\at\;the\;positions\;as\;shown\\in\;the\;figure.\;If\;the\;meter\\rule\;is\;balanced\;at\;its\\centre\;of\;gravity\;(C.G),\;find\\the\;unknown\;weight\;w.$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\w_1\;=\;4\;N\\\\d_1\;=30\;cm\;=\;\frac{30}{100}m\;=\;0.3\;m\\\\d_2\;=40\;cm\;=\;\frac{40}{100}m\;=\;0.4\;m\\\\w\;=\;?\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol w}_{\boldsymbol1}\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}{\boldsymbol d}_{\boldsymbol1}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol w\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}{\boldsymbol d}_{\boldsymbol2}\;\\\\4\;N\;\times\;0.3\;m\;=\;w\;\times\;0.4\;m\\\\w\;=\;\frac{4\;N\;\times\;0.3\;m}{0.4\;m}\\\\w\;=\;3\;N\\\\\\$$
====================================================================================
$$4.4\;\;\;A\;sea-saw\;is\;balanced\\with\;two\;children\;sitting\;near\\either\;end.\;Child\;A\;weighs\\30\;kg\;and\;sits\;2\;metres\;away\\from\;the\;pivot,\;while\;child\;B\\weighs\;40\;kg\;and\;sits\;1.5\\metres\;from\;the\;piovt.\\Calculate\;the\;total\;moment\\on\;each\;side\;and\;determine\\if\;sea-saw\;is\;in\;eqilibrium.$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Mass\;of\;chlid\;A\;=\;m_1\;=\;30\;kg\\\\Mass\;of\;chlid\;B\;=\;m_1\;=\;40\;kg\\\\Dis\tan ce\;of\;child\;A\;from\;pivot\;=l_1\;=\;2\;m\\\\Dis\tan ce\;of\;child\;B\;from\;pivot\;=l_2\;=\;1.5\;m\\\\Moment\;of\;child\;A\;=\;\tau_1\;=\;?\\\\Moment\;of\;child\;A\;=\;\tau_2\;=\;?\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\\boldsymbol T\boldsymbol o\boldsymbol r\boldsymbol q\boldsymbol u\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol\tau\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol F\\\boldsymbol T\boldsymbol o\boldsymbol r\boldsymbol q\boldsymbol u\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol\tau\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol W\\\boldsymbol T\boldsymbol o\boldsymbol r\boldsymbol q\boldsymbol u\boldsymbol e\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol\tau\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol m\boldsymbol g\\\\Moment\;of\;child\;A\;=\boldsymbol\;{\boldsymbol\tau}_{\mathbf1}\;=\;l_1\;\times\;F_1\\\\=\;l_1\times w_1=l_1\;\times\;m_1\;g=(2\;m)\times(30\;kg)(10\;m\;s^{-2})\\\\=\;(2\;m)\times(300\;kg\;m\;s^{-2})\;=\;600\;Nm\\\\\\Moment\;of\;child\;B\;=\;{\boldsymbol\tau}_{\mathbf2}\;=\;l_2\;\times\;F_2\\\\=\;l_2\times w_2=l_2\;\times\;m_2\;g=(1.5m)\times(40\;kg)(10\;m\;s^{-2})\\\\=\;(1.5\;m)\times(400\;kg\;m\;s^{-2})\;=\;600\;Nm\\\\\\\;Since\;\boldsymbol{\mathit\;}{\boldsymbol\tau}_{\boldsymbol1\boldsymbol{\mathit\;}}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol\tau}_{\boldsymbol2\boldsymbol{\mathit\;}}\\Therefore\;system\;is\;in\;equilibrium.\\$$
====================================================================================
$$4.5\;\;\;A\;crowbar\;is\;used\;to\\lift\;a\;box\;as\;shown\;in\;the\\figure.\;If\;the\;downward\\force\;of\;250\;N\;is\;applied\\at\;the\;end\;of\;the\;bar,\;how\\much\;weight\;does\;the\\other\;end\;bear\;?\;The\\crowbar\;has\;negligible\;weight.$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Downward\;force\;=\;{\boldsymbol F}_{\mathbf w}\;=\;250\;N\\\\Dis\tan ce\;of\;downward\;force\;=\;d_w\;=\;30\;cm\\\\=\;\frac{30}{100}\;m\;=\;0.3\;m\\\\Required\;weight\;(\;Force\;)\;=\boldsymbol\;\boldsymbol F\;=\;?\\\\Dis\tan ce\;of\;required\;force\;=\;d\;=\;5\;cm\\\\=\;\frac5{100}\;m\;=\;0.05\;m\\\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol\tau}_{\boldsymbol1}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol\tau}_{\boldsymbol2}\boldsymbol{\mathit\;}\\{\boldsymbol d}_{\boldsymbol w}\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}{\boldsymbol F}_{\boldsymbol w}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol d\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol F\boldsymbol{\mathit\;}\\\\\boldsymbol{\mathit(}0.3\;m)\;\times(250\;N)\;=\;(0.05\;m)\;\times\;\boldsymbol F\;\\\\\boldsymbol F\;=\;\frac{\boldsymbol{\mathit(}0.3\;m)\;\times(250\;N)\;}{0.05\;m}\;\\\\\boldsymbol F\;=\;1500\;N\\\\$$
====================================================================================
$$4.6\;\;\;\;A\;\mathit{30}\mathit\;cm\;long\;spanner\\is\;used\;to\;open\;the\;nut\;of\\a\;car.\;If\;the\;torque\;required\\for\;it\;is\;\mathit{150}\mathit\;N\mathit\;m,\;how\;much\\force\;F\;should\;be\;applied\\on\;the\;spanner\;as\;shown\\in\;the\;figure\;below.\\\\\\\\$$

$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\\\Length\;of\;spanner\;=\;l\;=\;30cm\\\\\frac{30\;}{100}\;m\;=\;0.3\;m\\\\Torque\;=\boldsymbol{\mathit\;}\boldsymbol\tau\;=\;150\;N\;m\\\\Force\;=\boldsymbol{\mathit\;}\boldsymbol F\;=\;?\\\\\\\\$$
$$\boldsymbol f\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol\tau\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol l\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\times}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol F\\\\150\;N\;m\;=\;\;0.3\;m\;\times\;\boldsymbol F\\\\\boldsymbol F\boldsymbol\;=\;\frac{150\;N\;m}{0.3\;m}\boldsymbol\;\\\\\boldsymbol F\;=\;500\;N\\\\\\\\$$
====================================================================================
$$4.7\;\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}\boldsymbol{\mathit\;}A\;5\;N\;ball\;hanging\\from\;a\;rope\;is\;pulled\;to\\the\;right\;by\;a\;horizontal\\force\;F.\;This\;rope\;makes\\an\;angle\;of\;60^\circ\;with\;the\\ceiling,\;as\;shown\;in\;the\\given\;figure.\;Determine\\the\;magnitude\;of\;force\;F\\and\;tension\;T\;in\;the\;string.\\\\\\\\$$
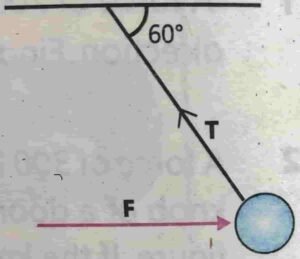
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\\\Weight\;of\;ball\;=\boldsymbol\;\boldsymbol w\;=?\;\\\\Angle\;=\;\theta\;=\;60\;degree\\\\Force\;=\;\boldsymbol F\;=?\\\\Tension\;=\;T\;=?\\\\\\\\\\$$
$$\boldsymbol F\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol w\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf5\boldsymbol\;\boldsymbol N\\\\\boldsymbol V\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol i\boldsymbol c\boldsymbol a\boldsymbol l\boldsymbol l\boldsymbol y\\\\T_y\;=\;w\\\\\boldsymbol T\boldsymbol\;\boldsymbol s\boldsymbol i\boldsymbol n\boldsymbol\;\boldsymbol\theta\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol w\\\\\boldsymbol T\;\sin\;60\;=\;5\;N\\\\\boldsymbol T\;(\frac{\sqrt3}2)\;=\;5\;N\\\\\boldsymbol T\;=\;\frac{5\;N}{\frac{\sqrt3}2}\\\\\boldsymbol T\;=\;\frac{10}{\sqrt3}N\\\\\boldsymbol T\boldsymbol\;=\;5.77\;N\\\\\\\boldsymbol H\boldsymbol o\boldsymbol r\boldsymbol i\boldsymbol z\boldsymbol o\boldsymbol n\boldsymbol t\boldsymbol a\boldsymbol l\boldsymbol l\boldsymbol y\boldsymbol\;\\\\\\\boldsymbol F\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol T\boldsymbol\;\boldsymbol c\boldsymbol o\boldsymbol s\boldsymbol\;\boldsymbol\theta\\\\\boldsymbol F\;=\;5.77\;N\;\times\;0.5\;\\\\\boldsymbol F\;=\;2.89\;N\\\\\\\\\\\\$$
====================================================================================
$$4.8\;\;\;A\;sign\;board\;is\\suspended\;by\;mans\\of\;two\;steel\;wires\;as\\shown\;in\;the\;given\;figure.\\If\;the\;weight\;of\;the\;board\\is\;200\;N,\;what\;is\;the\\tension\;in\;the\;strings\;?$$
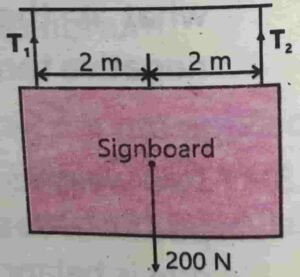
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\weight\;=\;w\;=\;200\;N\\\\Tension\;is\;1st\;string\;=\;T_1\;=\;?\\\\Tension\;is\;2nd\;string\;=\;T_2\;=\;?$$
$$Vertical\;forces\;will\;balance\;each\;other\\\\{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol+\boldsymbol\;{\boldsymbol T}_{\mathbf2}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{200}\boldsymbol\;\boldsymbol N\\\\Wires\;are\;symmetrically\;placed.\\\\Hence\;\\\\{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol T}_{\mathbf2}\boldsymbol\;\\\\So\\{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol+\boldsymbol\;{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf{200}\boldsymbol\;\boldsymbol N\\\\2{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol\;=\;200\;N\\\\{\boldsymbol T}_{\mathbf1}\;=\;\frac{\;200\;N}2\\\\{\boldsymbol T}_{\mathbf1}\;=\;100\;N\\\\But\\{\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol T}_{\mathbf2}\\\\So\;\\\\{\boldsymbol T}_{\mathbf2}\;=\;100\;N\\\\\\\\$$
$$Hence\;tension\;in\;each\;string\;in\;\boldsymbol{100}\boldsymbol{\mathit\;}\boldsymbol N\\\\\\\\$$
====================================================================================
$$4.9\;\;\;One\;girl\;0f\;30\;kg\\mass\;sits\;1.6\;m\;\;from\\the\;axis\;of\;see\;saw.\\Another\;girl\;of\;mass\\40\;kg\boldsymbol\;wants\;to\;sit\;on\\the\;other\;side,\;so\;that\\the\;see\;saw\;may\;remain\\in\;equilibrium.\;how\;for\\away\;from\;the\;axis,\;the\\other\;girl\;may\;sit\;?\\\\\\\\$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Mass\mathit\;of\mathit\;\mathit1st\mathit\;girl\mathit\;\mathit=\mathit\;m_{\mathit1}\mathit\;\mathit=\mathit\;\mathit{30}\mathit\;kg\\\\Mass\mathit\;of\mathit\;\mathit1st\mathit\;girl\mathit\;\mathit=\mathit\;m_{\mathit2}\mathit\;\mathit=\mathit\;\mathit{40}\mathit\;kg\\\\Dis\mathit{tan}ce\mathit\;of\mathit\;\mathit1st\mathit\;girl\mathit\;from\mathit\;axis\mathit\;\mathit=\mathit\;d_{\mathit1}\mathit\;\mathit=\mathit\;\mathit1\mathit.\mathit6\mathit\;m\\\\Distance\mathit\;of\mathit\;\mathit2nd\mathit\;girl\mathit\;from\mathit\;axis\mathit\;\mathit=\mathit\;d_{\mathit2}\mathit\;\mathit=\mathit\;\mathit?\\\\\\\\$$
$$\boldsymbol C\boldsymbol o\boldsymbol n\boldsymbol d\boldsymbol i\boldsymbol t\boldsymbol i\boldsymbol o\boldsymbol n\boldsymbol{\mathit\;}\boldsymbol f\boldsymbol o\boldsymbol r\boldsymbol{\mathit\;}\boldsymbol e\boldsymbol q\boldsymbol u\boldsymbol i\boldsymbol l\boldsymbol i\boldsymbol b\boldsymbol r\boldsymbol i\boldsymbol u\boldsymbol m\\Clockwise\;moment\;=\;Anticlockwise\;moment\\\\\\\\$$
$${\boldsymbol m}_{\mathbf1}\boldsymbol\;{\boldsymbol d}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol m}_{\mathbf2}\boldsymbol\;{\boldsymbol d}_{\mathbf2}\boldsymbol\;\\(30\;kg\;)\;(1.6\;m)\;=\;(40\;kg)\;d_2\\d_2\;=\;\frac{(30\;kg\;)\;(1.6\;m)}{40\;kg}\\{\boldsymbol d}_{\mathbf2}\;=\;1.2\;m\\Second\;girl\;should\;sit\;1.2\;m\;from\;axis\\\\\\\\$$
====================================================================================
$$4.10\;\;\;\;\;Find\;the\;tension\\in\;each\;string\;as\;shown\\in\;the\;given\;figure,\;if\;the\\block\;weighs\;\;\mathit{150}\mathit\;N.\\\\\\\\$$
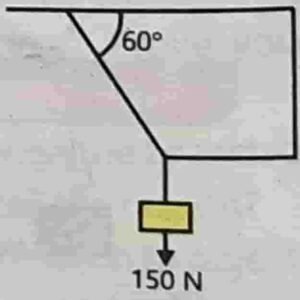
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\;\\weight\;=\;w\;=\;150\;N\\\\Tension\;in\;first\;string\;=\;T_1\;=\;?\\\\Tension\;in\;seconds\;string\;=\;T_2\;=\;?\\\\\\\\$$
$$After\;resolving\;into\;horizontal\;and\;vertical\;components\\\\$$
$$T_1\;\sin\;60\;+\;T_2\;\sin\;0\;=\;150\;N\\\\T_1\;(\frac{\sqrt3}2)\;+\;T_2\;(\;0\;)\;=\;150\;N\\\\T_1\;=\;150\;\times\;\frac2{\sqrt3}\\\\T_1\;=\;\frac{300}{\sqrt3}\;\\\\{\boldsymbol T}_{\boldsymbol1}\;=\;173.2\;N\\\\\\$$
$${\boldsymbol T}_{\mathbf1}\boldsymbol\;\boldsymbol c\boldsymbol o\boldsymbol s\boldsymbol\;\mathbf{60}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol T}_{\mathbf2}\boldsymbol\;\boldsymbol c\boldsymbol o\boldsymbol s\boldsymbol\;\mathbf0\\\\(173.20)\;(0.5)\;=\;T_2\;(\;1\;)\\\\{\boldsymbol T}_{\mathbf2}\;=\;86.6\;N\\$$
====================================================================================
Check! Some important links below
View All Physics Class 9th New Book 2025 Numerical with Solutions You tube videos for 9th Class Sir Najam Home page Notespunjab.com




