10th math paper 2025

10th math paper 2025 solution

(Section-I)

Q2.

Write short answers of any six from the following.

(i):- Solve by factorization.  5x² = 30x

5x² – 30x = 0

5x(x-6) = 0

5x=o or x-6 =0

x=0 or x=6

Solution Set ={ 0,6}

———————————————————–————–

(ii):- Define reciprocal equation and write an examples.

An equation is called Reciprocal equation, if it remains unchanged,

when x is replaced by 1/x.

For example

$2x^4 – 5x^3 – 14x^2 + 2$

——————————————————–—————–

(iii):- Write in standard form $$\frac1{x+4}+\;\frac1{x+4}\;=\;3$$

$$(x+4)\;(x-4)\;(\frac1{x+4}+\frac1{x-4})\;=\;(x+4)(x-4)\;3\\(x+4)\;(x-4)(\frac1{x+4})\;+\;(x+4)\;(x-4)(\frac1{x-4})\;=(\;x^2\;-\;16\;)\;3\\x-4\;+\;x+4\;=\;3\;x^2\;-48\\2x\;=\;3\;x^2\;-48\\0=\;3\;x^2\;-48\;-2x\\3\;x^2\;-\;2x\;-\;48\;=\;0$$

———————————————————-—————

(iv):- Find the discriminant.

$4x^2 + 10x + 2 = 0$

a = 4 , b = 10 , c = 2

$$\$\$Discriminant\backslash ;=\backslash ;b^2-4ac\backslash \backslash Discriminant\backslash ;=\backslash ;10^2-4(4)(2)\backslash \backslash Discriminant\backslash ;=\backslash ;100-32\backslash \backslash Discriminant\backslash ;=\backslash ;68\backslash \backslash \backslash \backslash \$\$$$ $$\Delta = b^2 – 4ac$$

————————————————————————-

(v):- Evaluate:-  $$\omega^{13}+\omega^{14}-5\\\omega^{12}\omega\;+\;\omega^{12}\;\omega^2\;-\;5\\(1)\;\omega\;+\;(1)\;\omega^2\;-\;5\\\omega\;+\;\omega^2\;-\;5\\-\;1\;-\;5\\-\;6\\$$ ${}^{\mathrm{}}$

————————————————————————-

(vi):- Form a Quadratic equation whose roots are 3 and 4.

S = sum of roots = 3+4 =7

P= Product of roots = (3)(4) = 12

x² – Sx + P = 0

x² -7x +12 = 0

————————————————————————-

(vii):- Find the value of x, if the ratios 2x+5 : 3x+4 and 3:4 are equal.

2x+5 : 3x+4 = 3:4

Product of means = Product of extremes

3( 3x+4 ) = 4 ( 2x+5 )

9x + 12 = 8x + 20

9x – 8x = 20 – 12

x = 8

————————————————————————-

(viii):- Define ratio and write an example

A ratio is a mathematical comparison of two or more quantities,

expressing how much one quantity is relative to another.

It is written in the form a:b.

For example 5meter ratio 7 meter and is written as 5:7

————————————————————————-

(ix):- Find the mean proportion between 20 and 45.

$$Mean\;Proportion\;=\;\sqrt{ab}\\Mean\;Proportion\;=\;\sqrt{20×45}\\Mean\;Proportion\;=\;\sqrt{900}\\Mean\;Proportion\;=\;30\\\\$$

====================================================================================

Q3.

Write short answers of any six from the following.

(i):- Resolve into partial fractions.

$$\frac{x-11}{(x-4)(x+3)}$$

$$\frac{x-11}{(x-4)\;(x+3)}=\;\frac A{x-4}+\frac B{x+3}\\x-11\;=\;A\;(x+3)\;+\;B\;(x-4)\\Put\;x+3\;=\;0\;i.e\;x=-3\;in\;the\;above\;equation\\-3-11\;=\;A\;(-3+3)\;+\;B(-3-4)\\-14\;=\;0\;+\;B(-7)\\\frac{-14}{-7}\;=\;B\\B\;=\;2\\x-11\;=\;A\;(x+3)\;+\;B\;(x-4)\\Put\;x-4=\;0\;i.e\;x=4\;\;in\;the\;above\;equation\\4-11\;=\;A\;(\;4+3)\;+B\;(4-4)\\-7\;=\;A\;(7)\;+\;0\\\frac{-7}7\;=\;A\\A\;=\;-1\\\frac{x-11}{(x-4)\;(x+3)}=\;\frac{-1}{x-4}+\frac2{x+3}$$

————————————————————————-

(ii):-  What are partial fractions ?

Partial fractions are components of a rational function that has been

decomposed into simpler fractions.

————————————————————————-

(iii):-  If A=N and B=W , Find A-B:

A = N = { 1,2,3,4,……..}  and  B = W = { 0,1,2,3,4,…….}

A-B = {  }

————————————————————————-

(iv):-  Find A x B if:  A = {0,2,5} , B = {-1,3}

A x B = { (0,-1) , (0,3) , (2,-1) , (2,3) , (5,-1) , (5,3)  }

————————————————————————-

(v):-  Find  $$X\;\cup\;Y\;\;if\;:\;X=\{1,7,9\}\;\;Y=\{2,4,5,9\}$$

XUY = {1,2,4,5,7,9}

————————————————————————-

(vi):-  Define an on function.

An onto function is a function where every output has at least one matching input. No output is left out.

OR

An onto function (or surjective function) is a function where every output has at least

one input that maps to it. In other words, every element in the codomain is used.

OR

An onto function (or surjective function) is a function where every element in

the codomain has at least one preimage in the domain.

OR

$$An\;onto\;function\;is\;a\;function\;where\;every\;element\;in\;the\;codomain\;has\;atleast\;one\;preimage\;in\;the\;domain\\A\;function\;f:A\rightarrow B\;is\;onto\;if,\;every\;element\;b\;in\;B\;,\;there\;exist\;one\;element\;a\;in\;A\\Such\;that\;f(a)=b\\\\$$

————————————————————————-

(vii):-  What do you mean by Harmonic Mean?

The Harmonic Mean is a type of average that is found by dividing the total number of values by

the sum of the reciprocals of those values.

$$H\;=\;\frac n{\displaystyle\underset{}{\sum\frac1{x_i}}}\\Where\;H\;i\;Harmonic\;mean\\n\;is\;total\;number\;of\;values\\x_i\;are\;the\;given\;values$$

————————————————————————-

(viii):-  Find Geometric mean of 2,4,8

$$If\;G\;is\;geometric\;Mean\;,\;then\\G\;=\;\sqrt[3]{2x4x8}\\G\;=\;\sqrt[3]{64}\\G\;=\;4\\$$

————————————————————————-

(ix):-  Find Median  1.9, 2.3, 2.5, 2.7, 2.9, 3.1

$$Median\;=\;\frac{2.5+2.7}2\\Median\;=\;\frac{5.2}2\\Median\;=\;\frac{2.6}2\\\\$$

====================================================================================

Q4.

Write short answers of any six from the following.

(i):- Define Quadrantal Angles. Give an example

$$A\;Quadrantal\;Angle\;is\;an\;angle\;whose\;Initial\;ray\;lies\;at\;positive\;x-axis\\and\;terminal\;ray\;lies\;on\;one\;of\;the\;coordinate\;axes\;(x-axis\;or\;y-axis)\\For\;example\;90\;degree.\;\\$$

(ii):- $$Convert\;into\;D\;M\;S\;form\;45.36\;degrees$$

$$45.36\;degree\;=\;45^{˚\;}\;{(0.36×60)}^´\\45.36\;degree\;=\;45^{˚\;}\;{(21.6)}^´\\45.36\;degree\;=\;45^{˚\;}\;21^´\;{(0.6×60)}^{”}\;45.36\;degree\;=\;45^{˚\;}\;21^´\;36^{”}\\$$

(iii):-  Convert Radian into degree:   3 radians.

$$\text{Degrees} = \text{Radians} \times \frac{180}{\pi}$$

For 3 radians:

$$3 \times \frac{180}{\pi} \approx 3 \times 57.2958 \approx 171.89^\circ$$

So, 3 radians ≈ 171.89°.

(iv):-  What is the circular measure of the angle between the hands of a watch at 6′ O clock?

$$Angle\;between\;two\;consective\;points\;=\;\frac{\mathrm\pi}6\;radian\\measure\;of\;the\;angle\;between\;the\;hands\;of\;a\;watch\;at\;6’\;O\;clock\\=(\;\frac{\mathrm\pi}6\;rad\;)\;(\;6\;)\\=\;\mathrm\pi\;\mathrm{radian}\\$$

To understand the next part  kindly  watch this video

(v):- Define an acute angle and give an example.

$$An\;acute\;angle\;is\;an\;angle\;that\;measures\\less\;than\;90^\circ\;(\frac{\mathrm\pi}2radians)\;but\;greater\;than\;0^\circ\;(0\;radian)\\For\;example\;\;30^\circ\;(\frac{\mathrm\pi}6\;radians)\\$$

(vi):- Define tangent of a circle.

The tangent of a circle is a straight line that touches the circle at exactly one point.

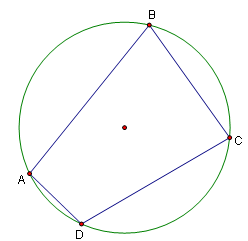
(vii):-  Define a cyclic quadrilateral and interpret it with diagram.

A quadrilateral that can be inscribed in a circle is called a cyclic quadrilateral.

(viii):- Define a Regular Polygon and give an example.

A regular polygon is a polygon in which all sides are equal in length and all interior angles are equal.

A square is a regular polygon.

(ix):- The length of sides of an equilateral triangle is 5.5 cm. What is its perimeter?

The perimeter of an equilateral triangle is given by the formula:

$$\text{Perimeter} = 3 \times \text{Side length}$$

Given that the side length is 5.5 cm, we calculate:

$$\text{Perimeter}=3\times 5.5=16.5\text{ cm}$$

(Section -II)

Note:  Attempt any three questions in all while Q.No 9 is compulsory.

Q5

(a):-  Solve the equation and check:  $$\sqrt{3x+100}\;-x\;=\;4$$

$$\sqrt{3x+100}\;-x\;=\;4\\\sqrt{3x+100}\;=\;x+4\\Taking\;square\;on\;both\;the\;sides\\({\sqrt{3x+100})\;}^2\;=\;{(x+4)}^2\\3x+100\;=\;x^2+2(x)(4)\;+4^2\\3x+100\;=\;x^2+\;8x\;+16\\3x+100\;-\;x^2-\;8x\;-16\;=\;0\\-x^2\;-5x\;+84\;=\;0\\-(x^2\;+\;5x\;-\;84)\;=\;0\\(x^2\;+\;5x\;-\;84)\;=\;0\\x^2\;+\;12x\;-7x\;-84\;=\;0\\x(x+12)-7(x+12)\;=0\\(x+12)\;(x-7)\;=\;0\\x+12\;=\;0\;\;or\;\;x-7=\;0\\x=\;-12\;\;\;or\;\;\;x=7\\Checking:-\\\sqrt{3x+100}\;-x\;=\;4\\put\;x=-12\\\sqrt{3(-12)+100}\;-(-12)\;=\;4\\\sqrt{-36+100}\;+12\;=\;4\\\sqrt{64}\;+12\;=\;4\\8+12\;=\;4\\20\;=\;4\\Which\;is\;false.\;Hence\;x=\;-12\;is\;an\;extraneous\;root.\\\sqrt{3x+100}\;-x\;=\;4\\put\;x=\;7\\\sqrt{3(7)+100}\;-7\;=\;4\\\sqrt{21+100}\;-7\;=\;4\\\sqrt{121}\;-7\;=\;4\\11-7=4\\4=4\\which\;is\;true.\;Hence\;x=7\;is\;a\;real\;root.\\Solution\;Set\;=\;\{\;7\;\}\\\\\\\\\\$$

====================================================================================

(b):- Solve by using synthetic division, if 2 is the root of equation. $$x^3\;-28x\;+\;48\;=0\\\\\\\\\\$$

$$Step\;1\;:-\\P(x)=x^3\;-28x\;+\;48\\\\\\\\\\$$

 

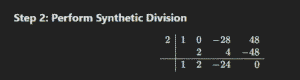
$$Step3:-\\Solve\;\;\;x^2+2x-24\;=\;0\\x^2+6x-4x-24=0\\x(x+6)-4(x+6)\;=\;0\\(x+6)(x-4)\;=\;0\\x+6\;=\;0\;\;\;or\;\;\;x-4\;=\;0\\x=-6\;\;or\;\;x=4\\Solution\;Set\;=\;\{2,4,-6\}\\\\\\\\\\$$

==============================================================================================================================

Q6

(a):-  Find x in Proportion.  8-x : 11-x  ::  16-x : 25-x

$$\\Products\;of\;means\;\;=\;\;Products\;of\;extremes\\(11-x)\;(16-x)\;=\;(8-x)\;(25-x)\\176-11x-16x+x^2\;=\;200-8x-25x+x^2\\176-27x\;=\;200\;-33x\\-27x+33x\;=\;200-176\\6x\;=\;24\\x\;=\;\frac{24}6\\x=4\\\\\\\\\\$$

====================================================================================

(b):-  Resolve into Partial fraction.  $$\frac{7x+4}{(3x+2)\;{(x+1)}^2}\\\\\\\\\\$$

$$\frac{7x+4}{(3x+2)\;{(x+1)}^2}\;=\;\frac A{3x+2}\;+\;\frac B{x+1}\;+\;\frac C{{(x+1)}^2}\\Multiplying\;both\;the\;sides\;by\;LCM\;i.e\;(3x+2)\;{(x+1)}^2\\7x+4\;=\;A\;{(x+1)}^2\;+\;B\;(3x+2)\;(x+1)\;+\;C\;(3x+2)\;\;\;……….\;Equ(i)\\Put\;3x+2\;=0\;\;in\;equation\;(i)\;\;\lbrack\;3x+2\;=\;0\;\;or\;3x=-2\;or\;x=\frac{-2}3\;\rbrack\\7(\frac{-2}3)\;+4\;=\;A\;{(\frac{-2}3+1)}^2\;+\;B\;(0)\;+\;C(0)\\\\\frac{-14}3+4\;=\;A\;{(\frac{-2+3}3)}^2\;\;\\\\\\\frac{-14+12}3\;=\;A{(\;\frac13)}^2\;\;\;\\\\\frac{-2}3=\;A(\;\frac19)\;\\\\\frac{-2}3(9)\;=\;A\;\\\\-2(3)\;=A\;\\\\A\;=\;-6\\\\\\\\$$

$$Put\;x+1\;=0\;\;in\;equation\;(i)\;\;\lbrack\;x=-1\rbrack\;\\7(-1)\;+4\;=\;A\;(0)+\;B\;(0)\;+\;C(3(-1)\;+2)\;\\-7+4\;=\;C(-3+2)\;\\-3\;=\;C(-1)\;\\\\\frac{-3}{-1}\;=\;C\;\\\\C=3\;\\\\\\\\\\\\$$

$$Expanding\;equation\;(i)\;\\\\7x+4\;=\;A\;(\;x^2\;+2x+1)\;+\;B\;(3\;x^2\;+2x\;+3x\;+2)\;+\;C\;(3x+2)\;\\\\Equating\;the\;coefficients\;of\;x^2\;\\\\0\;=\;A\;+\;3B\;\\\\After\;putting\;the\;value\;of\;A,\;we\;get\;\\\\0\;=\;-6\;+\;3B\;\\\\6\;=\;3B\;\\\\\frac63\;=\;B\;\\\\B\;=\;2\\\\\\\\\\\\$$

$$Hence\\\\\frac{7x+4}{(3x+2)\;{(x+1)}^2}\;=\;\frac{-6}{3x+2}+\;\frac2{x+1}\;+\;\frac3{{(x+1)}^2}\\\\\\\\\\\\$$

==============================================================================================================================

Q7

(a):-  $$Prove\;that\;\;B-A\;=\;B\cap A^c\;\;if;\\U\;=\;\{1,2,3,4………..,10\}\;\\A=\;\{1,3,5,7,9\}\;\\B\;=\;\{1,4,7,10\}\\\\\\\\\\\\$$

$$L.H.S\;=\;B-A\\L.H.S\;=\;\{1,4,7,10\}\;-\;\{1,3,5,7,9\}\\\\L.H.S\;\;=\;\{4,10\}\\\\A^c\;=\;U-A\\A^c\;=\;\{1,2,3,4,……,10\}\;-\;\{1,3,5,7,9\}\\\\A^c\;=\;\{2,4,6,8,10\}\\\\R.H.S\;=\;B\cap A^c\;\\R.H.S\;=\;\{1,4,7,10\}\;\cap\;\{2,4,6,8,10\}\;\\\\R.H.S\;=\;\{4,10\}\;\\\\Hence\;\;\;L.H.S\;=\;R.H.S\;\\\\\\$$

====================================================================================

Q7 (b):-  Determine standard deviation ‘S’ of the following set of numbers: 60,70,30,90,80,42

$$Number\;of\;terms\;=\;n\;=\;6\\\\X\;=\;60,70,30,90,80,42\;\;\\⅀X\;=\;60+70+30+90+80+42\;=372\;\;\;\\\\X^2\;=\;{(60)}^2,{(70)}^2,{(30)}^2,{(90)}^2,{(80)}^2,{(42)}^2\;\;\\X^2\;=\;3600,4900,900,8100,6400,1764\;\;\\\\⅀X^2\;=\;{(60)}^2+{(70)}^2+{(30)}^2+{(90)}^2+{(80)}^2+{(42)}^2\;\;\\⅀X^2\;=\;3600+4900+900+8100+6400+1764\;\;\\⅀X^2\;=\;25664\;\;\;\\\\S\tan derd\;Deviation\;=\;\sqrt{\frac{⅀X^2}n-\;{(\frac{⅀X}n)}^2}\;\;\\\\S\tan derd\;Deviation\;=\;\sqrt{\frac{25664}6-\;{(\frac{372}6)}^2}\;\\\\S\tan derd\;Deviation\;=\;\sqrt{4277.33-\;{(62)}^2}\;\;\\\\S\tan derd\;Deviation\;=\;\sqrt{4277.33-\;3844}\;\;\\\\S\tan derd\;Deviation\;=\;\sqrt{433.33}\;\\\\S\tan dard\;Deviation\;=\;20.82\\$$

==============================================================================================================================

Q8

(a):-  Find the remaining trigonometric functions if

$$CosecƟ\;=\;\frac{13}{12}\;\;and\;SecƟ\;>0\\$$

$$CosecƟ\;=\;\frac{13}{12}\;\\\Rightarrow\;SinƟ\;=\;\frac{12}{13}\;\;\\\Rightarrow\;Ɵ\;lies\;in\;2nd\;or\;\mathbf1\boldsymbol s\boldsymbol t\boldsymbol\;\boldsymbol Q\boldsymbol u\boldsymbol a\boldsymbol d\boldsymbol r\boldsymbol a\boldsymbol n\boldsymbol t\;\\\\and\;SecƟ\;>0\;\;\Rightarrow\;CosƟ\;>\;0\\\Rightarrow\;Ɵ\;lies\;in\;4th\;or\;\mathbf1\boldsymbol s\boldsymbol t\boldsymbol\;\boldsymbol Q\boldsymbol u\boldsymbol a\boldsymbol d\boldsymbol r\boldsymbol a\boldsymbol n\boldsymbol t.\\Hence\;Ɵ\;lies\;in\;\boldsymbol1\boldsymbol s\boldsymbol t\boldsymbol{\mathit\;}\boldsymbol Q\boldsymbol u\boldsymbol a\boldsymbol d\boldsymbol r\boldsymbol a\boldsymbol n\boldsymbol t.\\\\\\\\\\\\$$

$$\boldsymbol S\boldsymbol i\boldsymbol n^{\mathbf2}\boldsymbol Ɵ\boldsymbol\;\boldsymbol+\boldsymbol C\boldsymbol o\boldsymbol s^{\mathbf2}\boldsymbol Ɵ\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf1\boldsymbol\;\\\boldsymbol C\boldsymbol o\boldsymbol s^{\mathbf2}\boldsymbol Ɵ\boldsymbol\;\boldsymbol=\boldsymbol\;\mathbf1\boldsymbol\;\boldsymbol-\boldsymbol\;\boldsymbol S\boldsymbol i\boldsymbol n^{\mathbf2}\boldsymbol Ɵ\boldsymbol\;\\\\\boldsymbol C\boldsymbol o\boldsymbol s\boldsymbol Ɵ\boldsymbol\;\boldsymbol\;\boldsymbol=\boldsymbol\pm\boldsymbol\;\sqrt{\boldsymbol\;\mathbf1\boldsymbol\;\boldsymbol-\boldsymbol\;\mathbf S\mathbf i\mathbf n^{\mathbf2}\mathbf Ɵ}\boldsymbol\;\boldsymbol\;\\\\\boldsymbol C\boldsymbol o\boldsymbol s\boldsymbol Ɵ\boldsymbol\;\boldsymbol\;\boldsymbol=\boldsymbol\pm\boldsymbol\;\sqrt{\boldsymbol\;\mathbf1\boldsymbol\;\boldsymbol-{\boldsymbol(\boldsymbol\;\frac{\mathbf{12}}{\mathbf{13}}\boldsymbol)}^{\mathbf2}}\boldsymbol\;\boldsymbol\;\\\\\boldsymbol C\boldsymbol o\boldsymbol s\boldsymbol Ɵ\boldsymbol\;\boldsymbol\;\boldsymbol=\boldsymbol\pm\boldsymbol\;\sqrt{\boldsymbol\;\mathbf1\boldsymbol\;\boldsymbol-\frac{\mathbf{144}}{\mathbf{169}}}\boldsymbol\;\\\\\boldsymbol C\boldsymbol o\boldsymbol s\boldsymbol Ɵ\boldsymbol\;\boldsymbol\;\boldsymbol=\boldsymbol\pm\boldsymbol\;\sqrt{\boldsymbol\;\frac{\mathbf{169}\boldsymbol-\mathbf{144}}{\mathbf{169}}}\boldsymbol\;\\\\\boldsymbol C\boldsymbol o\boldsymbol s\boldsymbol Ɵ\boldsymbol\;\boldsymbol\;\boldsymbol=\boldsymbol\pm\boldsymbol\;\sqrt{\boldsymbol\;\frac{\mathbf{25}}{\mathbf{169}}}\boldsymbol\;\\\\\boldsymbol C\boldsymbol o\boldsymbol s\boldsymbol Ɵ\boldsymbol\;\boldsymbol\;\boldsymbol=\boldsymbol\pm\frac{\mathbf5}{\mathbf{13}}\boldsymbol\;\\\\\boldsymbol B\boldsymbol u\boldsymbol t\boldsymbol\;\boldsymbol\;\boldsymbol Ɵ\boldsymbol\;\boldsymbol l\boldsymbol i\boldsymbol e\boldsymbol s\boldsymbol\;\boldsymbol i\boldsymbol n\boldsymbol\;\mathbf1\boldsymbol s\boldsymbol t\boldsymbol\;\boldsymbol Q\boldsymbol u\boldsymbol a\boldsymbol d\boldsymbol r\boldsymbol a\boldsymbol n\boldsymbol t\boldsymbol.\boldsymbol\;\boldsymbol H\boldsymbol e\boldsymbol n\boldsymbol c\boldsymbol e\boldsymbol\;\\\boldsymbol\;\\\boldsymbol C\boldsymbol o\boldsymbol s\boldsymbol Ɵ\boldsymbol\;\boldsymbol\;\boldsymbol=\boldsymbol+\frac{\mathbf5}{\mathbf{13}}\boldsymbol\;\boldsymbol\;\\\\\boldsymbol\Rightarrow\boldsymbol\;\boldsymbol S\boldsymbol e\boldsymbol c\boldsymbol Ɵ\boldsymbol\;\boldsymbol\;\boldsymbol=\boldsymbol\;\frac{\mathbf{13}}{\mathbf5}\boldsymbol\;\\\\We\;know\;that\boldsymbol\;\boldsymbol\;\boldsymbol T\boldsymbol a\boldsymbol n\boldsymbol Ɵ\boldsymbol\;\boldsymbol\;\boldsymbol=\boldsymbol\;\frac{\mathbf S\mathbf i\mathbf n\mathbf Ɵ\boldsymbol\;}{\mathbf C\mathbf o\mathbf s\mathbf Ɵ\boldsymbol\;}\\\boldsymbol\;\boldsymbol T\boldsymbol a\boldsymbol n\boldsymbol Ɵ\boldsymbol\;\boldsymbol\;\boldsymbol=\boldsymbol\;\frac{{\displaystyle\frac{\mathbf{12}}{\mathbf{13}}}\boldsymbol\;}{{\displaystyle\frac{\mathbf5}{\mathbf{13}}}\boldsymbol\;}\boldsymbol\;\boldsymbol\;\\\\\boldsymbol T\boldsymbol a\boldsymbol n\boldsymbol Ɵ\boldsymbol\;\boldsymbol\;\boldsymbol=\boldsymbol\;\frac{\mathbf{12}\boldsymbol\;}{\mathbf5\boldsymbol\;}\boldsymbol\;\boldsymbol\;\\\boldsymbol\Rightarrow\\\boldsymbol C\boldsymbol o\boldsymbol t\boldsymbol Ɵ\boldsymbol\;\boldsymbol=\boldsymbol\;\frac{\mathbf5}{\mathbf{12}}\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\$$

====================================================================================

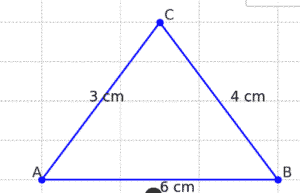
Q8(b):-  Escribe a Circle opposite to vertex A to a triangle ABC with sides

AB = 6cm , BC = 4cm  CA = 3cm

First we’ll draw triangle

Extend the sides AC and AB

 

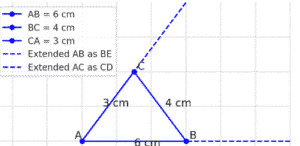
Bisect angle A

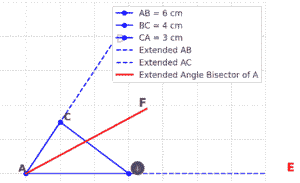
Now bisect angle DCB and angle EBC

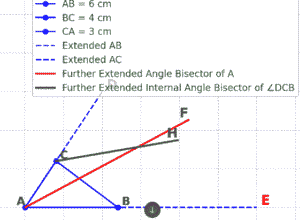
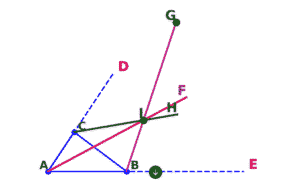
Now draw a perpendicular from point I on side on one of the extended sides.

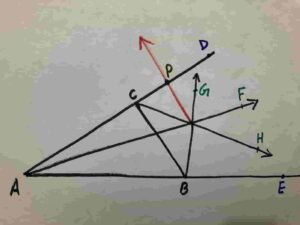
Then take I as centre draw a circle which will touch extended side internally and BC externally

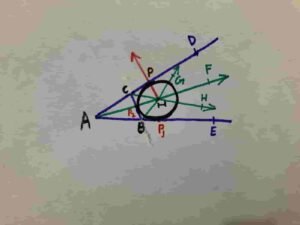
circle with radius IP is the required Escribed circle ( also called e circle ).

 

==================================================================

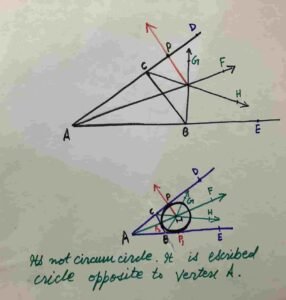
Q9:-

Prove that perpendicular from the centre of a circle on a chord bisects it.

Given:- AB is the chord of the circle with centre at O and OM is perpendicular to AB.

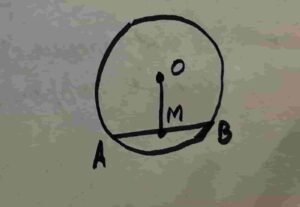
To Prove: Length of AM is equal to length of BM.

Construction: Join A and B with O.

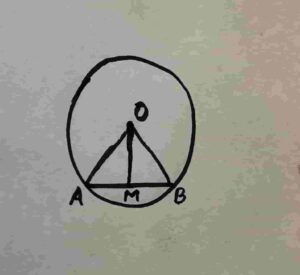
Proof:

=============================================================================================================================================

 Or

$$\boldsymbol P\boldsymbol r\boldsymbol o\boldsymbol v\boldsymbol e\boldsymbol\;\boldsymbol t\boldsymbol h\boldsymbol a\boldsymbol t\boldsymbol\;\boldsymbol o\boldsymbol p\boldsymbol p\boldsymbol o\boldsymbol s\boldsymbol i\boldsymbol t\boldsymbol e\boldsymbol\;\boldsymbol a\boldsymbol n\boldsymbol g\boldsymbol l\boldsymbol e\boldsymbol s\boldsymbol\;\boldsymbol o\boldsymbol f\boldsymbol\;\boldsymbol a\boldsymbol n\boldsymbol y\boldsymbol\;\boldsymbol q\boldsymbol u\boldsymbol a\boldsymbol d\boldsymbol r\boldsymbol i\boldsymbol l\boldsymbol a\boldsymbol t\boldsymbol e\boldsymbol r\boldsymbol a\boldsymbol l\boldsymbol\;\boldsymbol i\boldsymbol n\boldsymbol s\boldsymbol c\boldsymbol r\boldsymbol i\boldsymbol b\boldsymbol e\boldsymbol d\\\boldsymbol i\boldsymbol n\boldsymbol\;\boldsymbol a\boldsymbol\;\boldsymbol c\boldsymbol i\boldsymbol r\boldsymbol c\boldsymbol l\boldsymbol e\boldsymbol\;\boldsymbol a\boldsymbol r\boldsymbol e\boldsymbol\;\boldsymbol S\boldsymbol u\boldsymbol p\boldsymbol p\boldsymbol l\boldsymbol e\boldsymbol m\boldsymbol e\boldsymbol n\boldsymbol t\boldsymbol a\boldsymbol r\boldsymbol y$$

 

==============================================================================================================================

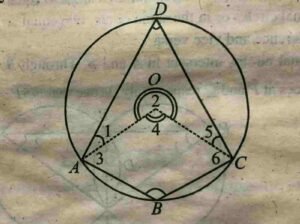
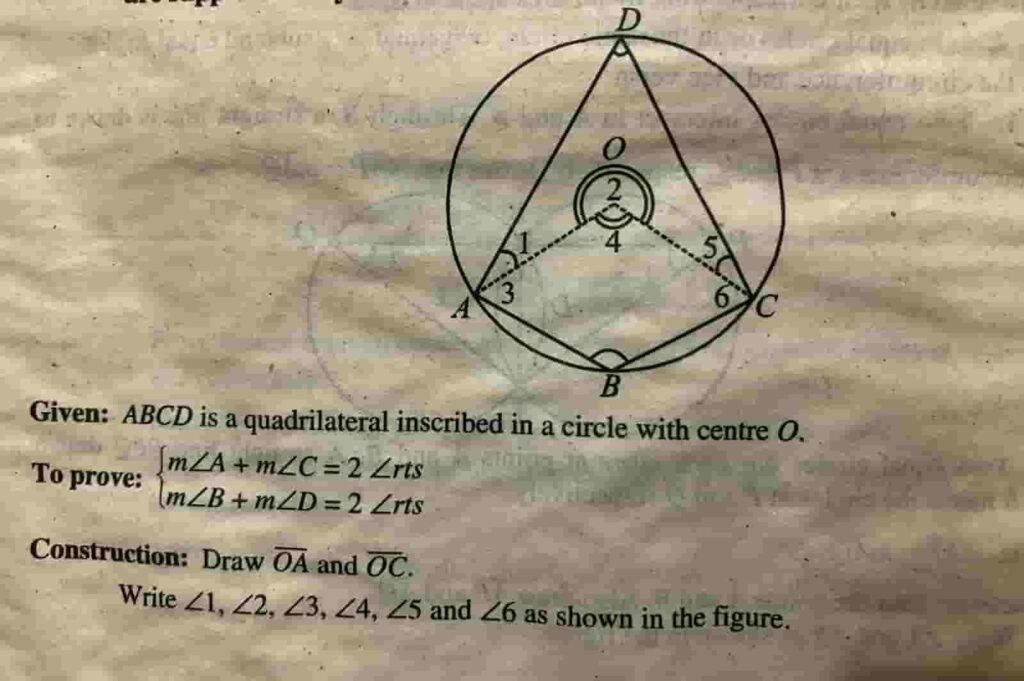
Ask any question regarding this paper in comment section. Enjoy 10th math paper 2025 solution

 

For New 9th you tube Channel Sir Najam

Home page notespunjab.com