Math 9th Chapter1 Notes | Real numbers
Math 9th Chapter1 Notes Exercise 1.1
9th Math Chapter1 Notes Real numbers. we will solve all exercises of first chapter of new syllabus developed by the government of the Punjab. we will try our best to give you written as well as visual solution. Here we will differentiate between rational and irrational numbers, properties equality and inequality of real numbers and how to insert rational numbers between two real numbers.
————————————————————————————————————————————————–
Q1:- Identify each of the following as rational or irrational number.
$$(i)\;\;2.353535\;\;Rational\\\\(ii)\;\;0.\overline6\;\;\;Rational\\\\(iii)\;\;2.636067….\;\;\;Irrational\\\\(iv)\;\;\sqrt7\;\;Irrational\\\\(v)\;\;e\;\;\;Irrational\\\\(vi)\;\;\mathrm\pi\;\;\mathrm{Irrational}\\\\(\mathrm{vii})\;\;5+\sqrt{11}\;\mathrm{Irrational}\\\\(\mathrm{viii})\;\sqrt3+\sqrt{13}\;\mathrm{Irrational}\\\\(\mathrm{ix})\;\;\frac{15}4\;\;\mathrm{Rational}\\\\(\mathrm x)\;\;(2-\sqrt2)\;(2+\sqrt2)\;=\;{(2)}^2\;-{(\sqrt2)}^2\\\;=4-2\;=\;2\;\;\;\mathrm{Rational}$$
————————————————————————————————————————————————–
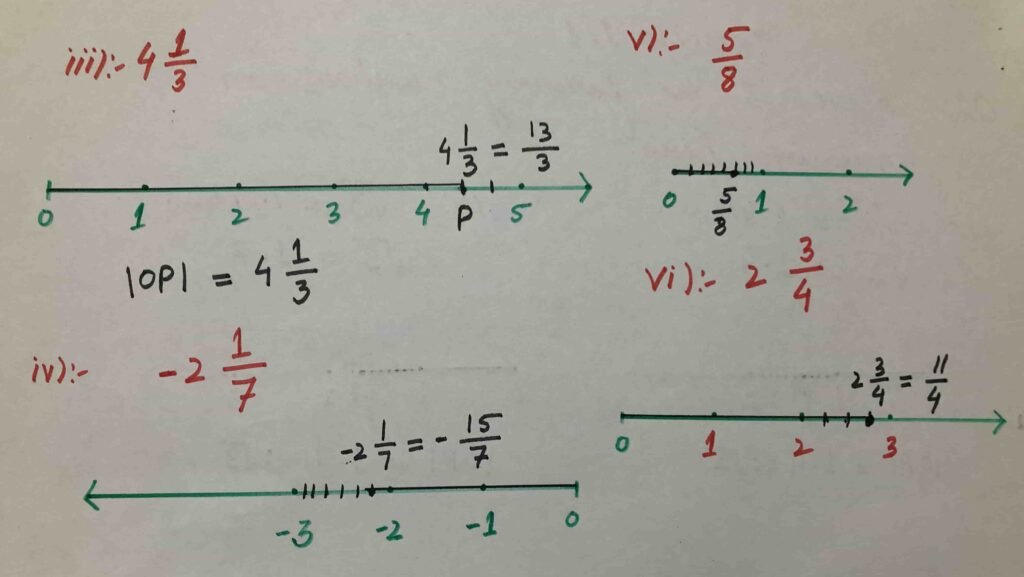
Q2:- Represent the following numbers on number line.
$$(i)\;\sqrt2\;\;\;\;(ii)\;\sqrt3\;\;\;\;(iii)\;4\frac13\;\;\\\\\;(iv)\;-2\frac17\;\;\;(v)\;\frac58\;\;\;(vi)\;\;2\frac34$$

————————————————————————————————————————————————–
Q3:- Express the following as rational numbers p/q where p and q are integers and q is not equal to zero.
$$(i)\;\;0\overline{.4}\\\\Let\;\;x\;=\;0\overline{.4}\\\\x=0.44444……\\\\Multiplying\;both\;the\;sides\;by\;10\\\\10x\;=\;4.44444……\\\\Subtracting\;x\;on\;both\;the\;sides\\\\10x-x\;=\;4.44444……\;-\;x\\\\9x\;=\;4.44444………\;-\;0.44444……..\\\\9x\;=\;4\\\\x=\frac49$$
$$(ii)\;\;0\overline{.37}\\\\Let\;\;x\;=\;0\overline{.37}\\\\x=0.373737……\\\\Multiplying\;both\;the\;sides\;by\;100\\\\100x\;=\;37.373737……\\\\Subtracting\;x\;on\;both\;the\;sides\\\\100x-x\;=\;37.373737……\;-\;x\\\\99x\;=\;37.373737………\;-\;0.373737……..\\\\99x\;=\;37\\\\x=\frac{37}{99}$$
$$(ii)\;\;0\overline{.21}\\\\Let\;\;x\;=\;0\overline{.21}\\\\x=0.212121……\\\\Multiplying\;both\;the\;sides\;by\;100\\\\100x\;=\;21.212121……\\\\Subtracting\;x\;on\;both\;the\;sides\\\\100x-x\;=\;21.212121……\;-\;x\\\\99x\;=\;21.212121………\;-\;0.212121……..\\\\99x\;=\;21\\\\x=\frac{21}{99}$$
————————————————————————————————————————————————–
Q4:- Name the property used in the following.
(i) (a+4) +b = a+(4+b)
Associative law of addition
————————————————————————-
(ii) Square root 2 + square root 3 = square root 3 + square root 2
Commutative law with respect to addition
————————————————————————-
(iii) x-x =0
Additive inverse
————————————————————————-
(iv) a( b + c ) = ab + ac
Left distributive law of multiplication over addition
————————————————————————-
(v) 16+0=16
Additive identity
————————————————————————-
(vi) 100×1=100
Multiplicative identity
————————————————————————-
(vii) 4 x ( 5 x 8 ) = ( 4 x 5 ) x 8
Associative law of multiplication
————————————————————————-
(viii) a b = b a
Commutative law with respect to multiplication
————————————————————————————————————————————————–
Q5:- Name the property used in the following.
$$(i)\;\;-3<-1\;\;\Rightarrow\;0<2\\\\\boldsymbol A\boldsymbol d\boldsymbol d\boldsymbol i\boldsymbol t\boldsymbol i\boldsymbol v\boldsymbol e\boldsymbol\;\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol p\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol y\\\\(ii)\;\;If\;a<b\;\;then\;\frac1a\;>\;\frac1b\\\\\boldsymbol R\boldsymbol e\boldsymbol c\boldsymbol i\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol c\boldsymbol a\boldsymbol l\boldsymbol\;\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol p\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol y\\\\(iii)\;\;\;If\;a<b\;\;then\;a\;+\;c\;<\;b\;+\;c\\\\\boldsymbol A\boldsymbol d\boldsymbol d\boldsymbol i\boldsymbol t\boldsymbol i\boldsymbol v\boldsymbol e\boldsymbol\;\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol p\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol y\\\\(iv)\;\;\;If\;ac<bc\;\;and\;c>0\;then\;a<b\\\\\boldsymbol D\boldsymbol i\boldsymbol v\boldsymbol i\boldsymbol s\boldsymbol i\boldsymbol o\boldsymbol n\boldsymbol\;\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol p\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol y\\\\(v)\;\;\;If\;ac<bc\;\;and\;c\;<\;0\;then\;a>b\\\\\boldsymbol D\boldsymbol i\boldsymbol v\boldsymbol i\boldsymbol s\boldsymbol i\boldsymbol o\boldsymbol n\boldsymbol\;\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol p\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol y\\\\(vi)\;\;Either\;\;a>b\;\;or\;a=b\;\;or\;a<b\\\\\boldsymbol T\boldsymbol r\boldsymbol i\boldsymbol c\boldsymbol h\boldsymbol o\boldsymbol t\boldsymbol o\boldsymbol m\boldsymbol y\boldsymbol\;\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol p\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol y$$
————————————————————————————————————————————————–
Q6:- Insert two rational numbers between (i) 1/3 and 1/4 (ii) 3 and 4 (iii) 3/5 and 4/5
$$(i)\;\;\frac13\;and\;\frac14\\Average\;of\;\;\frac13\;and\;\frac14=\;\frac{{\displaystyle\frac13}\;+\;{\displaystyle\frac14}}2=\frac{\displaystyle\frac{4+3}{12}}2=\frac7{24}\\\\Average\;of\;\;\frac7{24}\;and\;\frac14=\;\frac{\displaystyle\frac7{24}\;+\;\frac14}2=\frac{\displaystyle\frac{7+6}{24}}2=\frac{13}{48}\\\\Hence\;inserted\;rational\;numbers\;are\;\frac7{24}\;and\;\frac{13}{48}$$
————————————————————————-
$$(ii)\;\;3\;and\;4\\\\Average\;of\;3\;and\;4\;=\;\frac{3+4}2\;=\;\frac72\\\\Avarage\;of\;\frac72\;and\;4\;=\;\frac{{\displaystyle\frac72}\;+4}2\;=\;\frac{\displaystyle\frac{7+8}2}2\;=\;\frac{15}4$$
————————————————————————-
$$(iii)\;\;\frac35\;and\;\frac45\\Average\;of\;\;\;\frac35\;and\;\frac45=\;\frac{{\displaystyle\frac35}\;+\;{\displaystyle\frac45}}2=\frac{\displaystyle\frac{3+4}5}2=\frac7{10}\\\\Average\;of\;\;\;\frac7{10}\;and\;\frac45=\;\frac{\displaystyle\frac7{10}\;+\;\frac45}2=\frac{\displaystyle\frac{7+8}{10}}2=\frac{15}{20}\\\\Hence\;inserted\;rational\;numbers\;are\;\frac7{10}\;and\;\frac{15}{20}$$
Math 9th Chapter1 Notes Exercise 1.2
9th math ex1.2 new book notes. Lets check how to solve grade 9 math chapter 1 exercise 1.2. Class 9 math exercise 1.2 from the Punjab board’s new book is a part of chapter 1 and solution of real numbers will be explained here. why we use laws of indices to solve the questions? Lets first check what are radical expressions and then we will check about surds and its types. we will find that how to rationalize the denominator? How to simplify the sums with the help of laws of indices? you will be able to answer the above mentioned question after checking the written and visual solution of 9th math ex1.2.
————————————————————————————————————————————————–
Q 1 Rationalize the denominator of the following:
$$\boldsymbol(\boldsymbol i\boldsymbol)\boldsymbol\;\boldsymbol\;\frac{\mathbf{13}}{\mathbf4\boldsymbol+\sqrt{\mathbf3}}\\\\Rationalize\;with\;the\;conjugate\;of\;\\4+\sqrt3\;\;i.e\;\;4-\sqrt3\\\\\frac{13}{4+\sqrt3}\times\frac{4-\sqrt3}{4-\sqrt3}\\\\=\;\frac{3(4-\sqrt3)}{{(4)}^2\;-\;{(\sqrt3)}^2}\\\\=\;\frac{13(4-\sqrt{13})}{16-3}\\\\=\;\frac{13(4-\sqrt{13})}{13}\\\\=\;4-\sqrt{13}$$ $$\boldsymbol(\boldsymbol i\boldsymbol i\boldsymbol)\boldsymbol\;\boldsymbol\;\frac{\sqrt{\mathbf2}\boldsymbol\;\boldsymbol+\sqrt{\mathbf5}}{\sqrt{\mathbf3}}\\Rationalize\;with\;the\;\sqrt3\;\\\\\frac{\sqrt2\;+\sqrt5}{\sqrt3}\times\frac{\sqrt3\;}{\sqrt3}\\\\=\;\frac{(\sqrt2\;+\sqrt5)\;\sqrt3}{\;{(\sqrt3)}^2}\\\\\\=\;\frac{\sqrt6\;+\sqrt{15})}3$$ $$\boldsymbol(\boldsymbol i\boldsymbol i\boldsymbol i\boldsymbol)\boldsymbol\;\boldsymbol\;\frac{\sqrt{\mathbf2}\boldsymbol\;\boldsymbol-\mathbf1}{\sqrt{\mathbf5}}\\Rationalize\;with\;the\;\sqrt5\;\\\\\frac{\sqrt2\;-1}{\sqrt5}\times\frac{\sqrt5\;}{\sqrt5}\\\\=\;\frac{(\sqrt2\;-1)\;\sqrt5}{\;{(\sqrt5)}^2}\\\\\\=\;\frac{\sqrt{10}\;-\sqrt5)}5$$ $$\boldsymbol(\boldsymbol i\boldsymbol v\boldsymbol)\boldsymbol\;\boldsymbol\;\frac{\mathbf6\boldsymbol-\mathbf4\sqrt{\mathbf2}}{\mathbf6\boldsymbol+\mathbf4\sqrt{\mathbf2}}\\\\Rationalize\;with\;the\;conjugate\;of\\6+4\sqrt{2\;\;\;\;}\;i.e\;\;\;\;\;6-4\sqrt2\\\\\;\frac{6-4\sqrt2}{6+4\sqrt2}\times\;\frac{6-4\sqrt2}{6-4\sqrt2}\\\\=\;\;\frac{{(6-4\sqrt2)}^2}{{(6)}^2-{(4\sqrt2)}^2}\;\\\\=\;\frac{{(6)}^2+{(4\sqrt2)}^2-2(6)(4\sqrt2)}{36-(16\times2)}\\\\=\;\frac{36+(16\times2)-48\sqrt2}{36-32}\\\\=\;\frac{36+32-48\sqrt2}4\\\\=\;\frac{68-48\sqrt2}4\\\\=\;\frac{4(17-12\sqrt2)}4\\\\=\;17-12\sqrt2\\$$
$$\boldsymbol(\boldsymbol v\boldsymbol)\boldsymbol\;\boldsymbol\;\frac{\sqrt{\mathbf3}\boldsymbol-\sqrt{\mathbf2}}{\sqrt{\mathbf3}\boldsymbol+\sqrt{\mathbf2}}\\Rationalize\;with\;the\;conjugate\\of\;\sqrt3+\sqrt{2\;\;}\;i.e\;\;\;\sqrt3-\sqrt2\\\\\boldsymbol\;\frac{\sqrt3-\sqrt2}{\sqrt3+\sqrt2}\times\;\frac{\sqrt3-\sqrt2}{\sqrt3-\sqrt2}\\\\=\;\;\frac{{(\sqrt3-\sqrt2)}^2}{{(\sqrt3)}^2-{(\sqrt2)}^2}\;\\\\=\;\frac{{(\sqrt3)}^2+{(\sqrt2)}^2-2(\sqrt3)(\sqrt2)}{3-2}\\\\=\;\frac{3+2-2\sqrt6}1\\\\=\;\frac{5-2\sqrt6}1\\\\=\;5-2\sqrt6$$ $$\boldsymbol(\boldsymbol v\boldsymbol i\boldsymbol)\boldsymbol\;\boldsymbol\;\frac{\mathbf4\sqrt{\mathbf3}}{\sqrt{\mathbf7}\boldsymbol+\sqrt{\mathbf5}}\\Rationalize\;with\;the\;conjugate\\of\;\sqrt7+\sqrt{5\;}\;\;i.e\;\;\;\sqrt7-\sqrt5\\\\\boldsymbol\;\frac{4\sqrt3}{\sqrt7+\sqrt5}\times\;\frac{\sqrt7-\sqrt5}{\sqrt7-\sqrt5}\\\\\\=\;\;\frac{4\sqrt3(\sqrt7-\sqrt5)}{{(\sqrt7)}^2-{(\sqrt5)}^2}\;\\\\\\=\;\frac{{4(\sqrt{21}}-\sqrt{15})}{7-5}\\\\=\;\frac{{4(\sqrt{21}}-\sqrt{15})}2\\\\=\;{2(\sqrt{21}}-\sqrt{15})$$
————————————————————————————————————————————————–
Q 2 Simplify the following:
$$(i)\;\;\;{(\frac{86}{16})}^\frac{-3}4\\\\=\;\;{(\frac{16}{86})}^\frac34\;\\\\=\;\frac{{(16)}^\frac34}{\;{(86)}^\frac34}\\\\=\;\frac{{\;(2^4)}^{{}^\frac34}}{{(3^4)}^\frac34}\;\\\\=\;\frac{{(2)}^{4\times\frac34}}{{(3)}^{4\times\frac34}}\\\\=\;\frac{{(2)}^3}{{(3)}^3}\\\\=\;\frac8{27}\\$$
$$(ii)\;{\;\;\;\;\;(\frac34)}^{-2}\;\div\;\;{(\frac49)}^3\;\times\;\frac{16}{27}\\\\=\;{\;\;(\frac43)}^2\;\times\;\frac1{\;{(\frac49)}^{3\;}}\times\;\frac{16}{27}\\\\=\;\frac{16}9\times\frac1{\displaystyle\frac{64}{729}}\;\times\;\frac{16}{27}\\\\=\;\frac{16}9\times\frac{729}{\displaystyle64}\;\times\;\frac{16}{27}\\\\=\;12\\$$
$$(iii)\;\;\;{(0.027)}^\frac{-1}3\\\\=\;\;{(\frac{0027}{1000})}^\frac{-1}3\\\\=\;\;{(\frac{1000}{27})}^\frac13\\\\=\;\;\frac{{(10^3)}^{\displaystyle\frac13}}{{(3^3)}^\frac13}\\\\=\;\;\frac{\sqrt[3]{10^3}}{\sqrt[3]{3^3}}\\\\=\;\;\frac{10}3$$
$$(iv)\;\;\;\sqrt[7]{\frac{x^{14}\times y^{21}\times z^{35}}{y^{14}\;z^7}}\\\\=\;\;\sqrt[7]{x^{14}\times y^{21}\times z^{35}\;\times y^{-14}\times z^{-7}}\\\\=\;\;\sqrt[7]{x^{14}\times y^{21-14}\times z^{35-7}\;}\\\\=\;\;\sqrt[7]{x^{14}\times y^7\times z^{28}}\\\\=\;\;\sqrt[7]{x^{14}}\;\times\;\sqrt[7]{y^7}\;\times\;\sqrt[7]{z^{28}}\\\\=\;{(x^{14})}^\frac17\;\times\;\;{(y^7)}^\frac17\times\;\;{(z^{28})}^\frac17\\\\=\;{(x)}^{14\times\frac17}\times\;\;\;{(y)}^{7\times\frac17}\;\times\;\;{(z)}^{28\times\frac17}\\\\=\;x^2\;y\;z^4$$
$$(v)\;\;\;\frac{5.{(25)}^{n+1}-25.{(5)}^{2n}}{5.{(5)}^{2n+3}-{(25)}^{n+1}}\\\\=\;\;\frac{5.{(5^2)}^{n+1}-5^2\;{(5)}^{2n}\;}{5.{(5)}^{2n+3}\;-{(5^2)}^{n+1}}\\\\=\;\;\frac{5.{(5)}^{2(n+1)}-5^{2+2n}\;}{5^{1+2n+3}\;-{(5)}^{2(n+1)}}\\\\=\;\frac{5^{1+2n+2}-5^{2+2n}\;}{5^{4+2n}\;-5^{2n+2}}\\\\=\;\frac{5^{3+2n}-5^{2+2n}\;}{5^{4+2n}\;-5^{2n+2}}\\\\=\;\frac{5^{2n}(5^3-5^2)}{5^{2n}(5^4-5^2)}\\\\=\;\frac{(5^3-5^2)}{(5^4-5^2)}\\\\=\frac{125-25}{625-25}\\\\=\frac{100}{600}\\\\=\frac16\\$$
$$(vi)\;\;\;\frac{{(16)}^{x+1}+20(4^{2x})}{2^{x-3}\times8^{x+2}}\\\\\\=\;\;\frac{{(2^4)}^{x+1}+(2^2\times5^1){(2^2)}^{2x}}{2^{x-3}\times{(2^3)}^{x+2}}\\\\\\=\;\;\frac{{(2)}^{4(x+1)}+(2^2\times5^1){(2)}^{2(2x)}}{2^{x-3}\times{(2)}^{3(x+2)}}\\\\\\=\;\;\frac{2^{4x+4}+2^2\times5{\times2}^{4x}}{2^{x-3}\times2^{3x+6}}\\\\\\=\;\;\frac{2^{4x+4}+2^{2+4x}\times5}{2^{x-3+3x+6}}\\\\\\=\;\;\frac{2^{4x}(2^4+2^2\times5)}{2^{4x+3}}\\\\\\=\;\;\frac{16+4\times5}{2^3}\\\\\\=\;\;\frac{36}8\;=\;\frac92$$
$$(vii)\;\;\;\;\;\;\;{(64)}^\frac{-2}3\div\;\;{(9)}^\frac{-3}2\\\\=\;\;\;{(4^3)}^\frac{-2}3\div\;{(3^2)}^\frac{-3}2\\\\=\;\;4^{3\times\frac{-2}3}\div\;3^{2\times\frac{-3}2}\\\\=\;\;4^{-2}\;\div\;3^{-3}\\\\=\;\;4^{-2}\;\times\;3^3\\\\=\;\frac1{4^2}\times\;3^3\\\\=\;\frac{27}{16}\\$$
$$(viii)\;\;\;\frac{3^n\times\;9^{n+1}}{3^{n-1}\times\;9^{n-1}}\\\\=\;\;\frac{3^n\times\;{(3^2)}^{n+1}}{3^{n-1}\times\;{(3^2)}^{n-1}}\\\\=\;\;\frac{3^n\times\;{(3)}^{2(n+1)}}{3^{n-1}\times\;{(3)}^{2(n-1)}}\\\\=\;\;\;\frac{3^n\times\;{(3)}^{2n+2}}{3^{n-1}\times\;{(3)}^{2n-2}}\\\\=\;\;\frac{3^{n+2n+2}}{3^{n-1+2n-2}}\\\\=\;\;\frac{3^{3n+2}}{3^{3n-3}}\\\\=\;\;3^{3n+2}\;\times\;3^{-3n+3}\\\\=\;\;3^{3n+2-3n+3}\\\\=\;3^5\;=\;243\\$$
$$(ix)\;\;\;\frac{5^{n+3}-6\times5^{n+1}}{9\times5^n-4\times5^n}\\\\=\;\;\;\frac{5^{n+1}(5^2-6)}{5^n(9-4)}\\\\=\;\;\;\frac{5^{n+1}(25-6)}{5^n(5)}\\\\=\;\frac{5^{n+1}(19)}{5^{n+1}}\\\\=\;19$$
————————————————————————————————————————————————–
Q 3 $$x\;=\;3\;+\;\sqrt8\;\;\;\\\\Find\;the\;values\;of$$
$$x\;=\;3\;+\;\sqrt8\\(i)\;\;x+\frac1x\;=\;?\\Solution:\\x\;=\;3\;+\;\sqrt8\\\frac1x\;=\;\frac1{3\;+\;\sqrt8}\\\\$$
$$\frac1x\;=\;\frac1{3\;+\;\sqrt8}\times\frac{3\;-\;\sqrt8}{3\;-\;\sqrt8}\\\\\\\frac1x\;=\;\frac{3\;-\;\sqrt8}{{(3)}^2\;-\;{(\sqrt8)}^2}\\\\\frac1x\;=\;\frac{3\;-\;\sqrt8}{9\;-8}\\\\\frac1x=\;3\;-\;\sqrt8\\$$
$$x+\frac1x=\;3\;+\;\sqrt8\;+\;3\;-\;\sqrt8\\x+\frac1x=\;6$$
$$(ii)\;\;x-\frac1x=\;?\\\\\;\;x-\frac1x=\;3\;+\;\sqrt8\;-\;(\;3\;-\;\sqrt8\;)\\\\x-\frac1x=\;\;3\;+\;\sqrt8\;-\;\;3\;+\;\sqrt8\;\\\\x-\frac1x=\;\;2\sqrt8$$
$$(iii)\;\;\;\;x^2\;+\frac1{x^2}\;=\;?$$
$$x+\frac1x\;=\;6\\\\Taking\;square\;on\;both\;the\;sides\\\\\\{(x+\frac1x)}^2\;=\;{(6)}^2\\\\x^2+\frac1{x^2}+2\;=\;36\\\\x^2+\frac1{x^2}=\;36-2\\\\x^2+\frac1{x^2}=\;34\\\\$$
$$(iv)\;\;\;x^2-\;\frac1{x^2}\;=\;?\\We\;have\;already\;found\\\\x+\;\frac1x\;=\;\;6\\x-\frac1x\;=\;2\sqrt8\\\\Multiplying\;the\;above\;two\;equations\\\\(x+\;\frac1x)\;(x-\frac1x)\;=\;(6)\;(2\sqrt8)\\\\x^2\;-\;\frac1{x^2}\;=\;12\sqrt8\\\\$$
$$(v)\;\;\;x^4\;+\;\frac1{x^4}\;=\;?\\\\$$
$$We\;have\;already\;found\\\\x^2\;+\;\frac1{x^2}\;=\;34\\Taking\;square\;on\;both\;the\;side\\\\{(x^2\;+\;\frac1{x^2})}^2\;=\;{(34)}^2\;\;\\x^4\;+\;\frac1{x^4}\;+2\;=\;1156\\\\\\x^4\;+\;\frac1{x^4}\;\;=\;1156-2\\\\x^4\;+\;\frac1{x^4}\;\;=\;1154$$
$$(vi)\;\;\;{(x-\frac1x)}^2\;=\;?$$
$$We\;have\;already\;found\\\\x-\frac1x=2\sqrt8\\\\Taking\;square\;on\;both\;the\;sides\\\\\;{(x-\frac1x)}^2\;=\;{(2\sqrt8)}^2\;\;\;or\;\;{(x-\frac1x)}^2\;=\;4\times8\\\\\;{(x-\frac1x)}^2\;=\;32$$
————————————————————————————————————————————————–
Q 4 Find rational numbers p and q such that $$\frac{8-3\sqrt2}{4+3\sqrt2}\;=\;p\;+\;q\sqrt2$$
$$\frac{8-3\sqrt2}{4+3\sqrt2}\;=\;p\;+\;q\sqrt2\\\\Rationalize\;with\;the\;conjugate\;of\;4+3\sqrt2\\i.e\;\;\;\;4-3\sqrt2$$
$$\frac{8-3\sqrt2}{4+3\sqrt2}\;=\;p\;+\;q\sqrt2\\\\\frac{8-3\sqrt2}{4+3\sqrt2}\;\times\;\frac{4-3\sqrt2}{4-3\sqrt2}\;=\;p\;+\;q\sqrt2\\\\\frac{(8-3\sqrt2)\;(4-3\sqrt2)}{(4+3\sqrt2)\;(4-3\sqrt2)}\;=\;\;p\;+\;q\sqrt2\\\\\frac{32-24\sqrt2-12\sqrt2+9\sqrt4}{{(4)}^2\;-\;{(3\sqrt2)}^2}\;=\;p\;+\;q\sqrt2\\\\\frac{32-36\sqrt2+9(2)}{16-\;{(9\times2)}}\;=\;p\;+\;q\sqrt2\\\\\frac{32-36\sqrt2+18}{16-18}\;=\;p\;+\;q\sqrt2\\\\\frac{50-36\sqrt2}{-2}\;=\;p\;+\;q\sqrt2\\\\\frac{-2(-25+18\sqrt2\;)}{-2}\;=\;p\;+\;q\sqrt2\\\\-25+18\sqrt2\;=\;p\;+\;q\sqrt2\\\\Equating\\\\p\;=\;-25\;\;\;and\;\;\;q\;=\;18\\\\\\\\$$
————————————————————————————————————————————————–
Q 5 (Important question) Simplify the following:
$$\boldsymbol(\boldsymbol i\boldsymbol)\boldsymbol\;\boldsymbol\;\boldsymbol\;\boldsymbol\;\boldsymbol\;\frac{{\boldsymbol(\mathbf{25}\boldsymbol)}^{\displaystyle\frac{\mathbf3}{\mathbf2}}\boldsymbol\times\boldsymbol\;{\boldsymbol(\mathbf{243}\boldsymbol)}^{\displaystyle\frac{\mathbf3}{\mathbf5}}}{{\boldsymbol(\mathbf{16}\boldsymbol)}^{\displaystyle\frac{\mathbf5}{\mathbf4}}\boldsymbol\times{\boldsymbol(\mathbf8\boldsymbol)}^{\displaystyle\frac{\mathbf4}{\mathbf3}}}\\\\$$
$$=\;\frac{{(25)}^{\displaystyle\frac32}\times\;{(243)}^{\displaystyle\frac35}}{{(16)}^{\displaystyle\frac54}\times{\;(8)}^{\displaystyle\frac43}}\;\\\\=\frac{{(5^2)}^{\displaystyle\frac32}\times\;{(3^5)}^{\displaystyle\frac35}}{{(2^4)}^{\displaystyle\frac54}\times\;{{(2^3})}^{\displaystyle\frac43}}\\\\=\;\frac{{(5)}^{2\times{\displaystyle\frac32}}\times\;{\;{(3)}}^{5\times{\displaystyle\frac35}}}{{(2)}^{4\times{\displaystyle\frac54}}\times\;\;{(2)}^{3\times{\displaystyle\frac43}}}\\\\=\;\frac{5^3\;\times\;3^3}{2^5\;\times\;2^4}\\\;\\=\;\;\frac{125\;\times\;27}{32\;\times\;16}\\\\=\;\frac{3375}{512}$$
$$\boldsymbol(\boldsymbol i\boldsymbol i\boldsymbol)\boldsymbol\;\boldsymbol\;\boldsymbol\;\frac{\mathbf{54}\boldsymbol\;\boldsymbol\times\boldsymbol\;\sqrt[\mathbf3]{{\boldsymbol(\mathbf{27}\boldsymbol)}^{\mathbf2\mathbf x}}}{\mathbf9^{\mathbf x\boldsymbol+\mathbf1}\boldsymbol+\boldsymbol\;\mathbf{216}\boldsymbol\;\boldsymbol(\boldsymbol\;\mathbf3^{\mathbf2\mathbf x\boldsymbol-\mathbf1}\boldsymbol\;\boldsymbol)}$$
$$=\;\;\frac{54\;\times\;\sqrt[3]{{(27)}^{2x}}}{9^{x+1}+\;216\;(\;3^{2x-1}\;)}\;\\\\=\;\;\frac{2\times27\times\sqrt[3]{{(3}^3)^{2x}}}{{{(3}^2)}^{x+1}+8\times27\;(\;3^{2x-1}\;)\;}\\\\=\;\frac{2\times3^3\times\sqrt[3]{{(3)}^{3(2x)}}}{{(3)}^{2(x+1)}+2^3\times3^3(3^{2x-1}\;)\;}\\\\=\;\;\frac{2\times3^3\times{(3^{6x})}^{\displaystyle\frac13}}{{(3)}^{2x+2}+\;2^3\times{(3)}^{3+2x-1}}\\\\=\;\frac{2\times3^3\times{(3)}^{(6x)({\displaystyle\frac13})}}{{(3)}^{2x+2}+\;2^3\times{(3)}^{2x+2}}\\\\\\=\;\frac{2\times3^3\times{(3)}^{2x}}{{(3)}^{2x+2}(\;1+\;2^3\;)}\\\\=\;\frac{2\times{(3)}^{2x+3}}{{(3)}^{2x+2}(\;1+\;8\;)}\\\\=\;\frac{2\times{(3)}^{2x+2}\times3^1}{{(3)}^{2x+2}(\;9\;)}\\\\=\frac{2\times3}9\\\\=\;\frac23\\$$
$$\boldsymbol(\boldsymbol i\boldsymbol i\boldsymbol i\boldsymbol)\boldsymbol\;\boldsymbol\;\boldsymbol\;\boldsymbol\;\sqrt{\boldsymbol\;\frac{\boldsymbol\;{\boldsymbol(\mathbf{216}\boldsymbol)}^\frac{\mathbf2}{\mathbf3}\boldsymbol\times{\boldsymbol(\mathbf{25}\boldsymbol)}^\frac{\mathbf1}{\mathbf2}}{{\boldsymbol(\mathbf0\boldsymbol.\mathbf{04}\boldsymbol)}^\mathbf{\displaystyle\frac{-3}2}}}$$
$$=\;\;\;\sqrt{\;\frac{\;{(216)}^\frac23\times{(25)}^\frac12}{{(0.04)}^{\displaystyle\frac{-3}2}}}\;\\\\=\;\sqrt{\frac{{(6^3)}^\frac23\;\times\;{(5^2)}^\frac12\;}{\;{(\frac{004}{100})}^\frac{-3}2}}\\\\=\;\sqrt{\frac{{(6)}^{3\times{\displaystyle\frac23}}\;\times\;{(5)}^{2\times{\displaystyle\frac12}}\;}{\;{(\frac1{25})}^\frac{-3}2}}\\\\=\;\sqrt{\frac{{(6)}^{3\times{\displaystyle\frac23}}\;\times\;{(5)}^{2\times{\displaystyle\frac12}}\;}{\;{(\frac1{25})}^\frac{-3}2}}\\\\=\;\sqrt{\frac{6^2\;\times\;5}{\;{(25)}^\frac32}}\\\\=\;\sqrt{\frac{6^2\;\times\;5}{\;{(5^2)}^{\displaystyle\frac32}}}\\\\=\;\sqrt{\frac{6^2\;\times\;5}{\;{(5)}^{2\times{\displaystyle\frac32}}}}\\\\=\;\sqrt{\frac{6^2\;\times\;5}{\;5^3}}\\\\=\sqrt{\frac{36\;\times\;5}{\;125}}\\\\=\sqrt{\frac{36}{25}}\\\\=\;\frac65$$
$$\boldsymbol(\boldsymbol i\boldsymbol v\boldsymbol)\boldsymbol\;\boldsymbol(\boldsymbol a^\frac{\mathbf1}{\mathbf3}\boldsymbol+\boldsymbol b^\frac{\mathbf2}{\mathbf3}\boldsymbol)\boldsymbol\times\boldsymbol(\boldsymbol a^\frac{\mathbf2}{\mathbf3}\boldsymbol-\boldsymbol a^\frac{\mathbf1}{\mathbf3}\boldsymbol b^\frac{\mathbf2}{\mathbf3}\boldsymbol+\boldsymbol b^\frac{\mathbf4}{\mathbf3}\boldsymbol)\\$$
$$=(a^\frac13+b^\frac23)\;(a^\frac23-a^\frac13b^\frac23+b^\frac43)\\\\=a^\frac13(\;a^\frac23-a^\frac13b^\frac23+b^\frac34)\\+b^\frac23(a^\frac23-a^\frac13b^\frac23+b^\frac43)\\\\\\=a^\frac13a^\frac23-a^\frac13a^\frac13b^\frac23+a^\frac13b^\frac34\\+b^\frac23a^\frac23-b^\frac23a^\frac13b^\frac23+b^\frac23b^\frac43\\$$
‘$$=\;a^{\frac13+\frac23}-\;a^{\frac13+\frac13}b^\frac23+\;a^\frac13b^\frac34\;\\+\;\;b^\frac23a^\frac23-\;b^{\frac23+\frac23}a^\frac13+b^{\frac23+\frac43}\\\\\\=\;a^1-a^\frac23\;b^\frac23+a^\frac13b^\frac34\;\\+\;\;b^\frac23a^\frac23-\;b^\frac43\;a^\frac13\;+\;b^2\\$$
$$=\;a\;-\;a^\frac23\;b^\frac23\;+\;a^\frac13\;b^\frac43\;\\\;+\;a^\frac23\;b^\frac23\;-\;a^\frac13\;b^\frac43\;+\;b^2\;\\\\\\=a\;+\;b^2\\$$
Math 9th Chapter1 Notes Exercise 1.3
Usually students feel that word problems are difficult to solve. Lets start exercise 1.3 maths class9 in an easy way. Applications of real numbers in daily life are given in ex 1.3 of new book of grade 9 math for the students of Punjab. Students will check temperature conversion, profit and loss, find the numbers, find the ages of father and son and find the length in class 9 maths chapter 1 exercise 1.3 Punjab boards. Lets start carefully.
————————————————————————————————————————————————–
Q1 Sum of three consecutive integers if forty-two, find the three integers.
Let the integers are x, x+1 and x+2
x+x+1+x+2 = 42
3x+3 = 42
3x = 42-3
3x = 39
x= 13
Integers are 13,13+1 and 13+2 i.e 13,14 and 15.
————————————————————————————————————————————————–
Q2$$\;The\;diagram\;right\;angled\\triangle\;ABC\;in\;which\;the\\length\;of\;AC\;is\;\\(\sqrt3\;+\;\sqrt5\;)\;cm.\\The\;area\;of\;triangle\;ABC\\is\;(1+\sqrt{15}\;)\;cm^2.\;\;Find\\the\;length\;AB\;in\;the\\form\;(a\sqrt3\;+\;b\sqrt5\;)\;cm,\\where\;a\;\&\;b\;are\;integers.$$
$$Area\;of\;right\;triangle=\frac{Base\times Perpendicular}2\\\\1+\sqrt{15}=\frac{(\sqrt5\;+\;\sqrt3\;)\;(AB)}2\\\\\frac{2(1+\sqrt{15})}{\sqrt5\;+\;\sqrt3}=\;AB\\\\AB=\;\frac{2(1+\sqrt{15})}{\sqrt5\;+\;\sqrt3}\\\\Rationalize\;with\;\sqrt5\;-\;\sqrt3\\\\AB=\;\frac{2(1+\sqrt{15})}{\sqrt5\;+\;\sqrt3}\;\times\frac{\sqrt5\;-\;\sqrt3}{\sqrt5\;-\;\sqrt3}\\\\AB=\;\frac{2(1+\sqrt{15})\;(\sqrt5\;-\;\sqrt3)}{{(\sqrt5\;)}^2\;-\;{(\sqrt3)}^2}\\\\AB\;=\;\frac{2(\sqrt5-\sqrt3+\sqrt{75}-\sqrt{45})}{5-3}\\\\AB=\;\;\frac{2(\sqrt5-\sqrt3+\sqrt{25\times3}-\sqrt{9\times5})}2\\\\AB=\;\sqrt5-\sqrt3+5\sqrt3-3\sqrt5\\\\AB\;=4\sqrt5-\;2\sqrt5\\\\Hence,\;a=4\;,\;b=-2$$
————————————————————————————————————————————————–
Q3 $$\;\;A\;rec\tan gle\;has\;sides\\of\;length\;\;(2+\sqrt{18})\;m\\and\;\;(\;5-\frac4{\sqrt2})\;m.\\Epress\;the\;area\;of\\rectangle\;in\;the\;form\;of\\a+b\sqrt2,\;where\;a\;and\;b\\are\;integers$$
$$Let\\Length\;=L\;=\;(2+\sqrt{18})\;m\;\\Width\;=\;W\;=\;(\;5-\frac4{\sqrt2})\;m\\\\Area\;of\;rec\tan gle\;=\;LW\\\\Area\;of\;rec\tan gle\;=\;\;(2+\sqrt{18})\;(\;5-\frac4{\sqrt2})\\\\=10\;-\;\frac8{\sqrt2}\;+\;5\sqrt{18\;}-\;\frac{4\sqrt{18}}{\sqrt2}\\\\=\;10\;-\;\frac{8\;\sqrt2}{\sqrt2\;\sqrt2}+\;5\;\sqrt{9\times2}\;-\;4\sqrt{\frac{18}2}\\\\\\=10\;-\;\frac{8\;\sqrt2}2\;+\;5\;(3\sqrt2)\;-\;4\sqrt9\\\\=\;10-4\sqrt2+15\sqrt2\;-4(3)\\\\=10\;+11\sqrt2-12\\\\=\;-2\;+11\sqrt2\\\\Hence\;a=-2\;,\;b=11$$
————————————————————————————————————————————————–
Q4 Find two numbers whose sum is 68 and difference is 22
Let the numbers are x and y.
x + y = 68 and x – y = 22
Adding the above two equation, we get
x + y + x – y = 68 + 22
2x = 90
x = 45
Putting x = 45 in x + y = 68 , we get
45 + y = 68
y = 68 – 45
y = 23
Number are 45 and 23 whose sum is 68 and difference is 22.
————————————————————————————————————————————————–
Q5 Weather in Lahore was usually warm during the summer of 2024. The TV news reported temperature as high as 48 degree Celsius. By using the formula find the temperature as Fahrenheit scale.
$$Formula:\\F^\circ\;=\;\frac95C^\circ\;+\;32\\\\F^\circ\;=\;\;1.8(48)\;+\;32\\\\F^\circ\;=\;\;86.4\;+\;32\\\\F^\circ\;=118.4$$
————————————————————————————————————————————————–
Q6 Sum of ages of the father and son is 72 years. Six years ago, the father’s age was 2 times the age of the son. What was son’s age six years ago?
Let
Current age of father = F
Current age of son = S
F + S = 72 (i)
Six years ago
Age of father = F – 6
Age of son = S -6
F – 6 = 2 ( S – 6 ) or F – 6 = 2S – 12 or F – 2S = -12 + 6
F – 2S = -6 (ii)
Subtracting equation (ii) from equation (i)
F + S – ( F – 2S ) = 72 – (-6)
F + S – F + 2S = 72 + 6
3S = 78
Dividing both sides by 3
S = 26
Age of son 6 years ago = 26 – 6 = 20
Lets find age of father
Put S = 26 in equation (i)
F + 26 = 72 0r F = 72 – 26
Its mean F = 46
Putting F = 46 we get the age of father 6 years ago = 46 – 6 = 40
————————————————————————————————————————————————–
Q7 Mirha bought a toy for Rs 1520. What will the selling price be to get a 15% profit?
Purchased price = 1520 Rs
Profit Percentage = 15 %
Profit = 1520 ( 15 / 100 ) = 22800 / 100 = 228
Selling price = 1520 + 228 = 1748
————————————————————————————————————————————————–
Q8 Annual income of Tayyab is Rs 960000 while exempted amount is Rs 130000. How much tax would he have to pay at the rate of 0.75 % ?
Total amount = 960000 Rs
Exempted amount = 130000
Rate of tax = 0.75 %
Taxable amount = 960000 – 130000 = 830000
Tax = 830000 ( 0.75 % ) = 830000 ( 0.0075 ) = 6225 Rs
————————————————————————————————————————————————–
Q9 Find compound markup on Rs 375000 for one year at the rate of 14 % compounded annually.
Compound markup = 375000 ( 14 % ) = 375000 (0.14 ) = 52500 Rs
2nd method:-
$$A\;=\;P\;{(\;1+r\;)}^t\\\\A=375000\;{(1+14\;\%)}^1\;\\=\;375000\;(\;1+\;0.14\;)\\=\;375000\;(1.14)\;\\=\;427500\\$$
Markup = A – P = 427500 – 375000 = 52500 Rs
Math 9th Chapter1 Notes Review Exercise 1
9th Math Review Exercise1 2025 is an important exercise. In this exercise, we will review chapter 1 real numbers of math class 9. 1st question of the exercise is MCQs type and we will also solve the remaining short and long questions as well. We will check properties of equality and inequality of real numbers and different types of surds ?
————————————————————————-
Q1 Four options are given against each statement. Encircle the correct option.
————————————————————————————————————————————————–
i:-$$\sqrt7\;is$$
(a) integer (b) rational number (c) irrational number (d) natural number
$$\sqrt7\;is\;an\;irrational\;number$$
option c is correct.
7 is not a complete square.
————————————————————————-
ii:-$$\mathrm\pi\;\mathrm{and}\;\mathrm e\;\mathrm{are}$$
(a) natural numbers (b) integers (c) rational numbers (d) irrational numbers
$$\mathrm\pi\;\mathrm{and}\;\mathrm e\;\mathrm{are}\;\mathrm{irrational}\;\mathrm{numbers}$$
option d is correct.
$$\mathrm\pi\;=\;3.1416……………..\\\mathrm e\;=\;2.718281…………..\\\\\mathrm\pi\;\mathrm{and}\;\mathrm e\;\mathrm{are}\\\mathrm{non}\;\mathrm{repeating}\\\mathrm{and}\;\mathrm{non}\;\mathrm{terminating}\\\mathrm{decimal}\;\mathrm{numbers}\\$$
————————————————————————-
iii:-$$If\;n\;is\;not\;a\;perfct\;square,\\then\;\sqrt n\;is$$
(a) rational number (b) natural number (c) integer (d) irrational number
$$\sqrt n\;is\;an\;irrational\;number\;if\\n\;is\;not\;a\;perfect\;square$$
option d is correct.
$$\sqrt9\;is\;rational,\;9\;is\;perfect\;square.\\\sqrt7\;is\;irrational,\;7\;is\;not\;perfect\;square.\\$$
————————————————————————-
iv:-$$\sqrt3+\sqrt5\;is$$
(a) whole number (b) integer (c) rational number (d) irrational number
$$\sqrt3+\sqrt5\;is\;an\;irrational\;number$$
option d is correct
$$Sum\;of\;two\;rational\;numbers\;is\;a\\rational\;number.\;\sqrt3\;is\;a\;rational\\number.\;\sqrt5\;is\;a\;rational\;number.\\\sqrt3\;+\sqrt5\;is\;also\;a\;rational\;number.\\$$
————————————————————————-
v:-$$For\;all\;x\in\mathbb{R},\;x=x\;is\;called$$
(a) reflexive property (b) transitive number (c) symmetric property (d) trichotomy property
$$For\;all\;x\in\mathbb{R},\;x=x\;is\;called\\Reflexive\;property$$
option c is correct.
Every number is reflection of itself. 3 is reflection of 3, 4 is reflection of 4 and x is reflection of x.
————————————————————————-
vi:-$$Let\;a,b,c\;\in\mathbb{R},\;then\\a>b\;and\;b>c$$
$$\Rightarrow\;a>c\;is\;called$$
(a) trichotomy property (b) transitive property (c) additive property (d) multiplicative property
$$a>b\;and\;b>c\;\Rightarrow\;a>c\\is\;called\;transitive\;property$$
option b is correct
3 > 2 and 2 > 1 implies that 3 > 1
————————————————————————-
vii:-$$2^x\;\times\;8^x\;=\;64\;then\;x=$$
(a) 3/2 (b) 3/4 (c) 5/6 (d) 2/3
$$\;x=\frac32$$
option a is correct.
$$2^x\;\times\;8^x\;=\;64\\\\2^x\;\times\;{(2^3)}^x\;=\;2^6\\\\Rule\;of\;power\;of\;power\\\\2^x\;\times\;2^{3x}\;=\;2^6\\\\In\;multiplication\;Base\;same,\;powers\;add\\\\2^{x+3x}\;=\;2^6\\\\In\;equality,\;Base\;same,\;Powers\;same\\\\\Rightarrow\;x\;+\;3x\;=\;6\\\\4x\;=\;6\\\\x\;=\;\frac64\;=\;\frac32$$
————————————————————————-
viii:-$$Let\;a,b\;\in\mathbb{R},\;then\;a=b\\\;and\;b=a\;is\;called$$
(a) reflexive property (b) symmetric property (c) transitive property (d) additive property
$$a=b\;and\;b=a\;is\;called\;symmetric\;property$$
option b is correct.
Symmetric not reflexive, a and b are different, a=a means reflection.
————————————————————————-
ix:-$$\sqrt{75}\;+\;\sqrt{27}\;=$$
$$(a)\;\sqrt{102}\;\;\;(b)\;\;9\sqrt3\;\;\;(c)\;\;5\sqrt3\;\;\;(d)\;\;8\sqrt3$$
option d is correct.
$$\sqrt{75}\;+\;\sqrt{27}\;=\;5\sqrt3\;+\;3\sqrt3\;=\;8\sqrt3$$
————————————————————————-
x:-$$The\;product\;of\\(\;3+\sqrt5\;)\;(\;\;3-\sqrt5\;)\;is$$
(a) prime number (b) odd number (c) irrational number (d) rational number
$$(\;3+\sqrt5\;)\;(\;\;3-\sqrt5\;)\;is\;a\;rational\;number\\$$
option d is correct.
Product of irrational numbers may be rational or irrational number.
$$\;3+\sqrt5\;is\;irrational.\;\;3-\sqrt5\;is\;irrational\\\\(\;3+\sqrt5\;)\;(\;3-\sqrt5\;)\;=\;3^2\;-\;{(\sqrt5)}^2\\\\=\;9\;-\;5\;=\;4\\\\4\;is\;rational\;\Rightarrow(\;3+\sqrt5\;)\;(\;3-\sqrt5\;)\;is\;rational.$$
————————————————————————————————————————————————–
Q2 If a=3/2 , b=5/3 and c=7/5, then verify that
(i) a ( b + c ) = a b + a c
$$L.H.S\;=\;a\;(\;b\;+\;c\;)\\=\;\frac32\;(\;\frac53\;+\;\frac75\;)\\=\;\frac32\;(\;\frac{5\times5\;+\;7\times3}{15})\\=\;\frac32\;(\;\frac{25\;+\;21}{15})\\=\;\frac32\;(\frac{46}{15})\\=\frac{138}{30}\;=\;\frac{23}5$$
$$R.H.S\;=\;ab\;+\;ac\\=\;\frac32\times\frac53\;+\;\frac32\times\frac75\\=\;\frac52\;+\;\frac{21}{10}\\=\;\frac{5\times5\;+\;21\times1}{10}\\=\frac{25+21}{10}\\=\frac{46}{10}\;=\;\frac{23}5$$
L.H.S = R.H.S = 23/5
(ii) ( a + b ) c = a c + b c
$$L.H.S\;=\;(\;a\;+\;b\;)\;c\\=\;(\;\frac32\;+\;\frac53\;)\;\frac75\\=\;(\;\frac{3\times3\;+\;2\times5}6\;)\;\frac75\\=(\;\frac{9\;+10}6)\frac75\\=(\frac{19}6)\;\frac75\\=\;\frac{133}{30}$$
$$R.H.S\;=\;\;a\;c\;+\;b\;c\\=\;\frac32\times\frac75\;+\;\frac53\times\frac75\\=\;\frac{21}{10}\;+\;\frac73\\=\;\frac{3\times21\;+\;10\times7}{30}\\=\frac{63\;+\;70}{30}\\=\frac{133}{30}$$
L.H.S = R.H.S = 133/30
————————————————————————————————————————————————–
Q3 If a=4/3, b=5/2, c=7/4, then verify the associate property of real numbers w.r.t addition and multiplication.
Associate property of real numbers w.r.t addition is
a + ( b + c ) = ( a + b ) + c
$$L.H.S\;=\;a\;+\;(\;b\;+\;c\;)\\=\frac43\;+\;(\;\frac52\;+\;\frac74\;)\\=\;\frac43\;+\;(\;\frac{2\times5\;+\;1\times7}4)\\=\frac43+\;(\;\frac{10\;+\;7}4\;)\\=\frac43\;+\;\frac{17}4\\=\;\frac{4\times4\;+\;3\times17}{12}\\=\;\frac{16\;+\;51}{12}\\=\;\frac{67}{12}$$
$$R.H.S\;=(\;a\;+\;\;b\;)\;+\;c\;\\=(\;\frac43\;+\;\frac52\;)+\;\frac74\\=\;(\;\frac{2\times4\;+\;3\times5}6)\;+\;\frac74\\=\;(\frac{8+15}6)\;+\;\frac74\\=\;\frac{23}6+\frac74\\=\;\frac{2\times23\;+\;3\times7}{12}\\=\;\frac{46\;+\;21}{12}\\=\;\frac{67}{12}$$
L.H.S = R.H.S = 67/12
Associate property of real numbers w.r.t multiplication is
a ( b c ) = ( a b ) c
$$L.H.S\;=\;a\;(\;b\;c\;)\\=\;\frac43\;(\;\frac52\;\times\;\frac74\;)\\=\;\frac43\;(\;\frac{35}8\;)\\=\;\frac{35}6$$
$$R.H.S\;=\;(\;a\;b\;)\;c\\=(\;\frac43\;\times\;\frac52\;)\;\;\frac74\\=(\;\frac{10}3\;)\;\frac74\\=\;\frac{35}6$$
L.H.S = R.H.S = 35/6
————————————————————————————————————————————————–
Q4 Is 0 a rational number ? Explain.
Yes 0 is a rational number because 0 = 0.000………
Zero is non-terminating and non-recurring decimal number.
0 divided by any integer, other than 0,will give us 0. Hence, according to the definition of rational number, 0 is rational.
————————————————————————————————————————————————–
Q5 State trichotomy property of real numbers.
Trichotomy property:-
For all real numbers a and b
either a=b or a>b or a<b
————————————————————————————————————————————————–
Q6 Find two rational numbers between 4 and 5.
$$Average\;of\;4\;and\;5\;=\frac{4+5}2=\frac92\\Average\;of\;\frac92\;and\;5\;=\;\frac{{\displaystyle\frac92}+5}2\\=\frac{\displaystyle\frac{9+10}2}2=\frac{\displaystyle\frac{19}2}2=\frac{19}4$$
Hence required rational numbers are 9/2 and 19/4
————————————————————————————————————————————————–
Q7 Simplify the following:
(i) $$\sqrt[5]{\frac{x^{15}\;y^{35}}{z^{20}}}$$
$$=\;\sqrt[5]{\frac{\;{(x^3)}^5\;\;{(x^7)}^5}{\;{(z^4)}^5}}\\\\\\=\sqrt[5]{{\;(\frac{x^3\;x^7}{z^4})}^5}\\\\=\frac{x^3\;x^7}{z^4}$$
(ii) $$\sqrt[3]{{(27)}^{2x}}$$
$$=\;\sqrt[3]{{(3^3)}^{2x}}\\\\={\;(3^{6x})}^\frac13\\\\={(3)}^{6x\times\frac13}\\\\=3^{2x}$$
(iii) $$\frac{6\;{(3)}^{n+2}}{3^{n+1}\;-\;3^n}$$
$$=\;\frac{6\;{(3)}^n\;{(3)}^2}{3^n\;{(3)}^1\;-\;3^n}\\\\=\frac{6\;{(3)}^n\;9}{3^n\;{(\;(3)}^1\;-\;1\;)}\\\\=\frac{6\times9}{3-1}\\\\=\frac{54}2\\\\=27$$
————————————————————————————————————————————————–
Q8 The sum of three consecutive odd integers is 51. Find the three integers.
Let the three consecutive odd integers are 2x+1 , 2x+3 and 2x+5
According to the given condition.
2x+1 + 2x+3 + 2x+5 = 51
6x + 9 = 51 or 6x = 51-9 or 6x = 42
Dividing both the sides by 6
x = 42/6 = 7
Integers are
2x+1 = 2(7) +1 = 15
2x+3 = 2(7) + 3 = 17
2x+5 = 2(7) + 5 = 19
————————————————————————————————————————————————–
Q9 Abdullah picked up 96 balls and placed them into two buckets. One bucket has twenty-eight more balls than the other bucket. How many balls were in each bucket ?
Let the balls in 1st bucket = x
Let the balls in 2nd bucket = x+28
x+x+28 = 96
2x = 96-28
2x = 68
x = 34
Balls in 1st bucket = 34
balls in 2nd bucket = 34 + 28 = 62
————————————————————————————————————————————————–
Q 10$$Salma\;invested\;Rs\;3,50,000\\in\;a\;bank,\;which\;paid\\simple\;profit\;at\;the\;rate\;of\\7\frac14\;\%\;annum.\;After\;2\;years,\\the\;rate\;was\;increased\;to\\8\;\%\;per\;annum.\;Find\\the\;amount\;she\;had\;at\\the\;end\;of\;7\;years.\;$$
$$Total\;investment\;=\;3,50,000\\For\;1st\;year=3,50,000\times7\frac14\%\\=3,50,000\;\times\frac{29}4\;\%\\=3,50,000\;\times7.25\;\%\\=\;3,50,000\;\times\frac{725}{100}\;\%\\=3500\;\times725\%\\=3500\;\times\frac{725}{100}\\=\;35\;\times725\;=\;25375\;Rs\;$$
$$Investment\;for\;2nd\;year\\=\;25375\;\times2\;=\;50750\;Rs\\$$
$$Investment\;for\;3rd\;year\\=\;3,50,000\;\times\;8\;\%\\=\;3,50,000\;\times\frac8{100}\\=\;3500\;\times\;8\;=\;28000\\$$
$$Investment\;for\;last\;5\;years\\=\;28000\;\times\;5\\=\;140000\\$$
Total interest = 50750 + 140000 = 190750
Total amount = 350000 + 190750 = 540750
————————————————————————————————————————————————–
Check! some important link




