Math Class 9 New Book Exercise 1.1
Math Class 9 New Book Exercise 1.1.we will solve all exercises of first chapter of new syllabus developed by the government of the Punjab. we will try our best to give you written as well as visual solution. Here we will differentiate between rational and irrational numbers, properties equality and inequality of real numbers and how to insert rational numbers between two real numbers.
————————————————————————————————————————————————–
Q1:- Identify each of the following as rational or irrational number.
$$(i)\;\;2.353535\;\;Rational\\\\(ii)\;\;0.\overline6\;\;\;Rational\\\\(iii)\;\;2.636067….\;\;\;Irrational\\\\(iv)\;\;\sqrt7\;\;Irrational\\\\(v)\;\;e\;\;\;Irrational\\\\(vi)\;\;\mathrm\pi\;\;\mathrm{Irrational}\\\\(\mathrm{vii})\;\;5+\sqrt{11}\;\mathrm{Irrational}\\\\(\mathrm{viii})\;\sqrt3+\sqrt{13}\;\mathrm{Irrational}\\\\(\mathrm{ix})\;\;\frac{15}4\;\;\mathrm{Rational}\\\\(\mathrm x)\;\;(2-\sqrt2)\;(2+\sqrt2)\;=\;{(2)}^2\;-{(\sqrt2)}^2\\\;=4-2\;=\;2\;\;\;\mathrm{Rational}$$
————————————————————————————————————————————————–
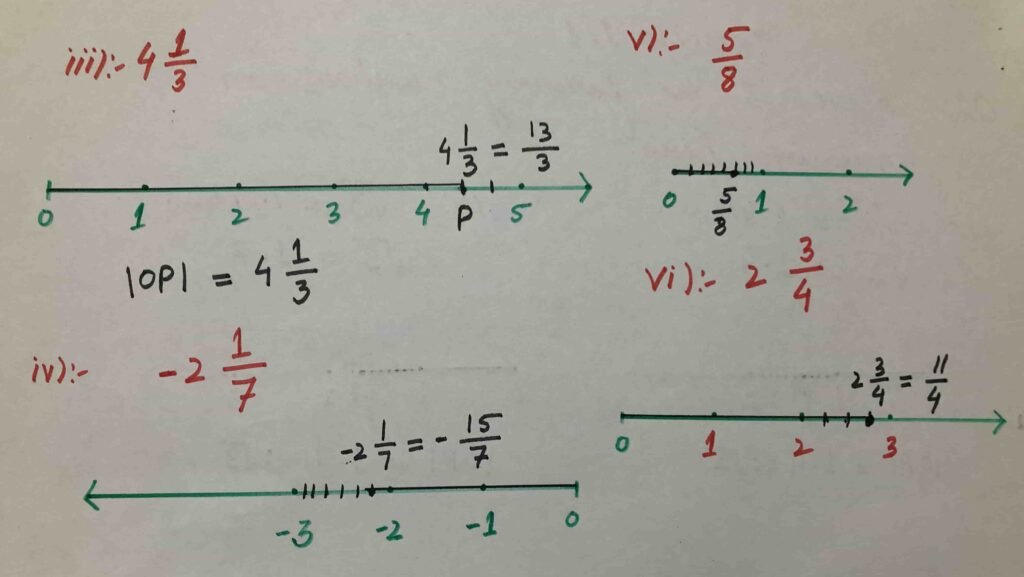
Q2:- Represent the following numbers on number line.
$$(i)\;\sqrt2\;\;\;\;(ii)\;\sqrt3\;\;\;\;(iii)\;4\frac13\;\;\\\\\;(iv)\;-2\frac17\;\;\;(v)\;\frac58\;\;\;(vi)\;\;2\frac34$$

————————————————————————————————————————————————–
Q3:- Express the following as rational numbers p/q where p and q are integers and q is not equal to zero.
$$(i)\;\;0\overline{.4}\\\\Let\;\;x\;=\;0\overline{.4}\\\\x=0.44444……\\\\Multiplying\;both\;the\;sides\;by\;10\\\\10x\;=\;4.44444……\\\\Subtracting\;x\;on\;both\;the\;sides\\\\10x-x\;=\;4.44444……\;-\;x\\\\9x\;=\;4.44444………\;-\;0.44444……..\\\\9x\;=\;4\\\\x=\frac49$$
$$(ii)\;\;0\overline{.37}\\\\Let\;\;x\;=\;0\overline{.37}\\\\x=0.373737……\\\\Multiplying\;both\;the\;sides\;by\;100\\\\100x\;=\;37.373737……\\\\Subtracting\;x\;on\;both\;the\;sides\\\\100x-x\;=\;37.373737……\;-\;x\\\\99x\;=\;37.373737………\;-\;0.373737……..\\\\99x\;=\;37\\\\x=\frac{37}{99}$$
$$(ii)\;\;0\overline{.21}\\\\Let\;\;x\;=\;0\overline{.21}\\\\x=0.212121……\\\\Multiplying\;both\;the\;sides\;by\;100\\\\100x\;=\;21.212121……\\\\Subtracting\;x\;on\;both\;the\;sides\\\\100x-x\;=\;21.212121……\;-\;x\\\\99x\;=\;21.212121………\;-\;0.212121……..\\\\99x\;=\;21\\\\x=\frac{21}{99}$$
————————————————————————————————————————————————–
Q4:- Name the property used in the following.
(i) (a+4) +b = a+(4+b)
Associative law of addition
————————————————————————-
(ii) Square root 2 + square root 3 = square root 3 + square root 2
Commutative law with respect to addition
————————————————————————-
(iii) x-x =0
Additive inverse
————————————————————————-
(iv) a( b + c ) = ab + ac
Left distributive law of multiplication over addition
————————————————————————-
(v) 16+0=16
Additive identity
————————————————————————-
(vi) 100×1=100
Multiplicative identity
————————————————————————-
(vii) 4 x ( 5 x 8 ) = ( 4 x 5 ) x 8
Associative law of multiplication
————————————————————————-
(viii) a b = b a
Commutative law with respect to multiplication
————————————————————————————————————————————————–
Q5:- Name the property used in the following.
$$(i)\;\;-3<-1\;\;\Rightarrow\;0<2\\\\\boldsymbol A\boldsymbol d\boldsymbol d\boldsymbol i\boldsymbol t\boldsymbol i\boldsymbol v\boldsymbol e\boldsymbol\;\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol p\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol y\\\\(ii)\;\;If\;a<b\;\;then\;\frac1a\;>\;\frac1b\\\\\boldsymbol R\boldsymbol e\boldsymbol c\boldsymbol i\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol c\boldsymbol a\boldsymbol l\boldsymbol\;\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol p\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol y\\\\(iii)\;\;\;If\;a<b\;\;then\;a\;+\;c\;<\;b\;+\;c\\\\\boldsymbol A\boldsymbol d\boldsymbol d\boldsymbol i\boldsymbol t\boldsymbol i\boldsymbol v\boldsymbol e\boldsymbol\;\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol p\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol y\\\\(iv)\;\;\;If\;ac<bc\;\;and\;c>0\;then\;a<b\\\\\boldsymbol D\boldsymbol i\boldsymbol v\boldsymbol i\boldsymbol s\boldsymbol i\boldsymbol o\boldsymbol n\boldsymbol\;\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol p\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol y\\\\(v)\;\;\;If\;ac<bc\;\;and\;c\;<\;0\;then\;a>b\\\\\boldsymbol D\boldsymbol i\boldsymbol v\boldsymbol i\boldsymbol s\boldsymbol i\boldsymbol o\boldsymbol n\boldsymbol\;\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol p\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol y\\\\(vi)\;\;Either\;\;a>b\;\;or\;a=b\;\;or\;a<b\\\\\boldsymbol T\boldsymbol r\boldsymbol i\boldsymbol c\boldsymbol h\boldsymbol o\boldsymbol t\boldsymbol o\boldsymbol m\boldsymbol y\boldsymbol\;\boldsymbol p\boldsymbol r\boldsymbol o\boldsymbol p\boldsymbol e\boldsymbol r\boldsymbol t\boldsymbol y$$
————————————————————————————————————————————————–
Q6:- Insert two rational numbers between (i) 1/3 and 1/4 (ii) 3 and 4 (iii) 3/5 and 4/5
$$(i)\;\;\frac13\;and\;\frac14\\Average\;of\;\;\frac13\;and\;\frac14=\;\frac{{\displaystyle\frac13}\;+\;{\displaystyle\frac14}}2=\frac{\displaystyle\frac{4+3}{12}}2=\frac7{24}\\\\Average\;of\;\;\frac7{24}\;and\;\frac14=\;\frac{\displaystyle\frac7{24}\;+\;\frac14}2=\frac{\displaystyle\frac{7+6}{24}}2=\frac{13}{48}\\\\Hence\;inserted\;rational\;numbers\;are\;\frac7{24}\;and\;\frac{13}{48}$$
————————————————————————-
$$(ii)\;\;3\;and\;4\\\\Average\;of\;3\;and\;4\;=\;\frac{3+4}2\;=\;\frac72\\\\Avarage\;of\;\frac72\;and\;4\;=\;\frac{{\displaystyle\frac72}\;+4}2\;=\;\frac{\displaystyle\frac{7+8}2}2\;=\;\frac{15}4$$
————————————————————————-
$$(iii)\;\;\frac35\;and\;\frac45\\Average\;of\;\;\;\frac35\;and\;\frac45=\;\frac{{\displaystyle\frac35}\;+\;{\displaystyle\frac45}}2=\frac{\displaystyle\frac{3+4}5}2=\frac7{10}\\\\Average\;of\;\;\;\frac7{10}\;and\;\frac45=\;\frac{\displaystyle\frac7{10}\;+\;\frac45}2=\frac{\displaystyle\frac{7+8}{10}}2=\frac{15}{20}\\\\Hence\;inserted\;rational\;numbers\;are\;\frac7{10}\;and\;\frac{15}{20}$$
————————————————————————————————————————————————–
Best of luck for your bright future. Remember me in your prayers. Check! some useful links.
————————————————————————————————————————————————–




