Physics 9th New Book | Chapter2 Notes
Physics 9th New Book Chapter2 MCQs. short questions, long questions and numerical will be solved.
9th Physics New Book Chapter 2 MCQs
Tick the correct answer.
2.1 The numerical ratio of displacement to distance is:
(a) always less than one (b) always equal to one (c) always greater than one (d) equal to or less than one
Option (d) is correct.
Explanation:-
Because displacement is the shortest distance so, distance will always be equal or greater than the displacement.
If motion is in straight line, ration between displacement and distance will be 1.
But, if displacement is less than distance, that is motion is curved, numerical ratio of displacement to distance will also be less than 1.
————————————————————————————————————————————————–
2.2 If a body does not change its position with respect to some fixed point, then it will be in a state of:
(a) rest (b) motion (c) uniform motion (d) variable motion
Option (a) is correct
Explanation:-
Rest means object is not changing its position with respect to its surroundings
————————————————————————————————————————————————–
2.3 A boll is dropped from the top of a tower, the distance covered by it in the first second is:
(a) 5 m (b) 10 m (C) 50 m (d) 100 m
Option ( a ) is correct.
Explanation:-
$$Initial\;velocity=v_i=\;0\\Acceleration=g=10\;ms^{-2}\\Time\;=\;t\;=\;1\;s\\Dis\tan ce\;=\;S\;=\;?$$
FORMULA:- $$S\;=\;v_it\;+\frac12gt^2$$
$$S\;=(0)\;(1)+\frac12(10)\;{(1)}^2\\\\S\;=\;5\;m$$
————————————————————————————————————————————————–
2.4 A body accelerates from rest to a velocity of 144 Km in 20 second. The distance covered by it is:
(a) 100 m (b) 400 m (c) 1400 m (d) 1440 m
Option ( b ) is correct.
Explanation:-
$$Initial\;velocity=v_i=0\\\\Final\;velocity=v_f=144kmh^{-1}\\=144\;(\frac{1000}{3600})\;=\;40\;ms^{-1}\\\\Time\;=\;t\;=\;20\;s\\Dis\tan ce\;=\;S\;=\;?\\$$
FORMULA:- $$S\;=\;V_{av}\;\times\;t\\\\S\;=\;(\frac{v_i\;+\;v_f}2)\;t\\$$
$$After\;putting\;the\;values\\We\;get\\\\S\;=\;(\frac{0\;+\;40}2)\;(\;20\;)\\S\;=\;400\;m\\$$
————————————————————————————————————————————————–
2.5 A body is moving with constant acceleration starting from rest. It covers a distance S in 4 seconds. How much time does it take to cover one-fourth of this distance?
(a) 1 s (b) 2 s (c) 4 s (d) 16 s
Option ( b ) is correct.
Explanation:-
$$Initial\;velcoity=v_i=\;0\\\\Dis\tan ce\;=\;S\;=\;?\\\\\frac14S\;=\;S_1\;=\;?\\\\Time\;=\;t\;=\;4\;s\\\\Time\;for\;S_1\;=\;t_1\;=\;?$$
Formula:-
$$2nd\;equation\;of\;motion\\S\;=\;V_i\;t\;+\;\frac12\;a\;t^2$$
$$After\;putting\;the\;values\\We\;get\\\\S\;=\;0(4)\;+\;\frac12a{(4)}^2\\S\;=\;8\;a$$
$$Divding\;both\;the\\sides\;by\;4\\\\\frac S4=\;\frac{8\;a}4\\\\S_1\;=\;2\;a$$
Formula:-
Again We will use 2nd equation of motion
$$S_1\;=v_i\;t_1\;+\;\frac12\;a\;t_1^2\\$$
$$After\;putting\;the\;values\\We\;get\\\\2a\;=\;0(t_1)\;+\;\frac12a\;\;t_1^2\\4\;=\;\;t_1^2\\\\taking\;square\;root\\on\;both\;ths\;side\\\\\pm2\;=\;t_1\\\\Time\;starts\;from\;0\\So,\;we\;will\;neglect\\the\;negative\;sign\\\\t_1\;=\;2\;s\\$$
————————————————————————————————————————————————–
2.6 The displacement time graphs of two objects A and B are shown in the figure. Point out the true statement from the following:
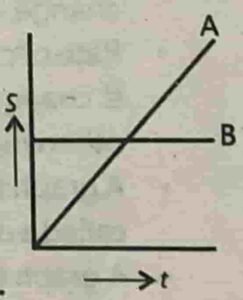
(a) The velocity of A is greater than B. (b) The velocity of A is less than B. (c) The velocity of A is equal to that of the B. (d) The graph gives no information in this regard.
Option ( a ) is correct.
Explanation:-
Line of object B is parallel to t-axis, so object B is at rest.
Line of object B shows that its distance is uniformly increasing with respect to time, so its speed is increasing.
————————————————————————————————————————————————–
2.7 The area under the speed-time graph is numerically equal to:
(a) velocity (b) uniform velocity (c) acceleration (d) distance covered
Option ( d ) is correct.
Explanation:-
Because S = V t. Distance is equal to the product of speed and time.
————————————————————————————————————————————————–
2.8 Gradient of the speed-time graph is equal to:
(a) speed (b) velocity (c) acceleration (d) distance covered
Option ( c ) is correct.
Explanation:-
Gradient means slope which is ration between rise and run.
Speed divided by time gives us acceleration.
So, gradient of speed-time graph gives acceleration.
————————————————————————————————————————————————–
2.9 Gradient of distance time graph is equal to
(a) speed (b) velocity (c) distance covered (d) acceleration
Option ( b ) is correct.
Explanation:-
Gradient means slope which is ration between rise and run.
Distance divided by time gives us speed.
So, gradient of distance-time graph gives speed. If distance is displacement, we will get velocity.
————————————————————————————————————————————————–
2.10 $$A\;car\;accelerates\;uniformly\\from\;80.5\;km\;h^{-1}\;at\;t\;=\;0\\to\;113\;km\;h^{-1}\;at\;t\;=\;9s\\Which\;graph\;best\;describes\\the\;motion\;of\;the\;car\;?$$
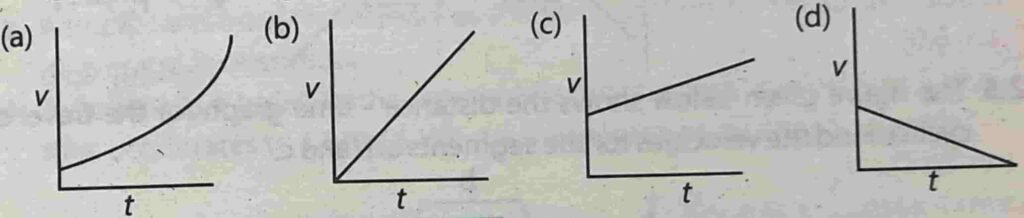
Option ( c ) is correct.
Explanation:-
After converting the speeds in meters per second, we get 22.36 meters at t=0 and 31.39 m at t=9.
So graph graph will not start from origin, Option b is incorrect.
Its speed is increasing, so option d is also incorrect.
In option a there is no straight line, so its also incorrect.
When we plot the graph of ( 0 , 22.36 ) and ( 9 , 31.39 ), we get option c
————————————————————————————————————————————————–
Physics 9th New Book Chapter2 Short Questions
2.1 Define scalar and vector quantities.
Page 29
Scalar
A scalar is that physical quantity which needs magnitude only to describe it completely.
Vector
A vector is that physical quantity which needs magnitude as well as direction to describe it completely.
————————————————————————————————————————————————–
2.2 Give 5 examples each for scalar and vector quantities.
Page 29
Examples of scalars are distance, speed, mass, time, temperature, and energy.
Examples of vector are displacement, velocity, acceleration, force, torque and momentum.
————————————————————————————————————————————————–
2.3 State head-to-tail rule for addition of vector.
Page 31
To add vectors, we apply a rule called head-to-tail rule.
Definition of head to tail rule.
To add vectors, we draw their representative lines such that the head of one line coincides with the tail of the other. The resultant vector is given by a single vector which is directed from the tail of the first vector to the head of the last vector.
————————————————————————————————————————————————–
2.4 What are distance-time graph and speed-time graph.
Page 39
Distance-time graph shows the relation between distance S and time t taken by a body.
We take time t along x-axis and distance s along y-axis
Gradient (slope) of distance-time graph gives us speed.
Page 42
Speed-time graph shows the relation between speed V and time t taken by a body.
We take time t along x-axis and speed v along y-axis
Gradient (slope) of speed-time graph gives us acceleration.
————————————————————————————————————————————————–
2.5 Falling objects near the Earth have the same constant acceleration. Does this imply that a heavier object will fall faster than a lighter object?
No, heavier object will not fall faster than a lighter object in the absence of air resistance.
Weight of any body will not affect the rate of free fall.
$$g\;=\;9.8\;m\;s^{-2}\;\approx\;10\;m\;s^{-2}$$
————————————————————————————————————————————————–
2.6 The vector quantities are sometimes written in scalar notation ( not bold face ). How is the direction indicated ?
Page 30
With the help of axes, we can indicate the direction of vector, even its written in scalar notation.
————————————————————————————————————————————————–
2.7 A body is moving with uniform speed. Will its velocity be uniform ? Given reason
If a body is moving with uniform speed, its velocity may or may not be uniform.
If a body is moving with uniform speed in straight line, its velocity is uniform but if its moving with uniform speed in curved path for example circle, its velocity will not be uniform because particle is changing its direction at every point.
————————————————————————————————————————————————–
2.8 Is it possible for a body to have acceleration? When moving (i) constant velocity (ii) constant speed
If a body is moving with constant velocity, its acceleration will be zero because its neither changing speed nor direction.
But if a body is moving with constant speed and its direction is also not changing, there will be no acceleration.
If a body is moving with constant speed but its direction is changing, its acceleration will not be zero.
Physics 9th New Book Chapter2 Long Questions
2.1 How a vector can be represented graphically? Explain.
We cannot represent a vector by a ray however, We represent a vector by a line segment with a arrow head on it.
The line segment represents the magnitude of that vector and the arrow head represents the direction of that vector.
The tail represents the initial point of that vector and the arrow head represents the final point as well as direction of that vector.
In the coordinate plane, initial point of vector will be at origin (0,0) and final point (x , y) can be anywhere in the plane.
Usually, We draw a vector from (0,0) to (x , y). In two dimensional plane, we write vector A as A = (x , y) or A = xi + yj
We can also represent a vector by a bold face letter or an arrow head on it.
$$We\;can\;represent\\vector\;A\;as\\\boldsymbol A\boldsymbol\;\boldsymbol\;or\;\;\overrightarrow{A\;}$$
$$We\;can\;represent\;the\\magnitude\;of\;a\;vector\;A\;\\A\;or\;\;\left|\boldsymbol A\right|\;\;or\;\;\left|\overrightarrow{A\;}\right|\;$$
————————————————————————————————————————————————-
2.2 Differentiate between: (i) Rest and motion (ii) Speed and velocity
Rest
Rest means body is not changing its position with respect to its surrounding.
Motion
Motion means body is changing its position with respect to its surrounding.
A book at the table is at rest with respect to the table. A car moving on the road is in motion with respect to a man standing on the road.
But, rest and motion are relative concepts. We cannot say that about a body is completely in rest or in motion.
For example, a man in a moving train is in rest with respect to another man in the same train but both the men are in motion with respect to another man standing on the platform.
————————————————————————————————————————————————-
2.3 Describe different types of motion. Also give examples.
Generally there are three types of motion. 1 Translatory motion 2 Rotatory motion 3 Vibratory motion.
1 translatory motion:
Motion is translatory motion if every particle of body moves uniformly in the same direction. For example motion of car or train. There are three types of translatory motion.
1. Linear Motion : If the body moves along the straight line, it is called linear motion. for example a freely falling body.
2. Random Motion : If the body moves along an irregular path , the motion is called random motion. for example the motion of bee is random motion.
3. Circular Motion : Motion of the body along the circle is called circular motion. For example Ferris wheel.
2 Rotatory Motion :
Motion is rotatory motion if each point of body moves around a fixed point. For example motion of electric fan and motion of top.
3 Vibratory Motion :
Motion is vibratory motion if body repeats its to and fro motion about a fixed point. For example the motion of a pendulum.
————————————————————————————————————————————————–
2.4 Explain the difference between distance and displacement.
The distance is the length of actual path of the motion while displacement is the shortest length.
[table “11” not found /]————————————————————————————————————————————————–
2.5 What do gradients of distance-time graph and speed-time graph represent? Explain by drawing diagram.
Gradient is the measure of slope of line . Gradient of distance time graph is equal to the average speed of the body while gradient of speed time graph is equal to the acceleration of the body.
$$Slope=\frac{RQ}{PR}\\\;\;\;\;\;\;\;\;\;\;\;=\frac{S_2-S_1}{t_2-t_1}\\\;\;\;\;\;\;\;\;\;\;\;\;=\frac St=V_{av}\\Also\\\frac St=\tan\;\theta=slope$$
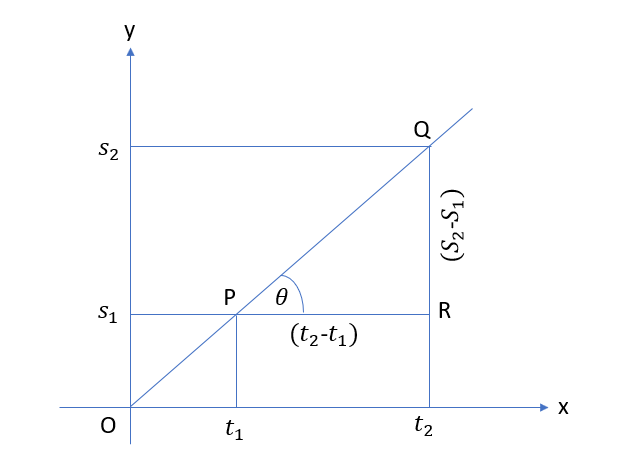
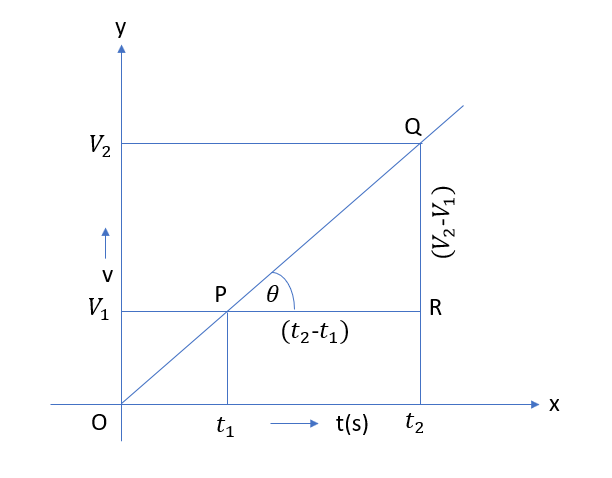
————————————————————————————————————————————————–
2.6 Prove that the area of under speed-time graph is equal to the distance covered by an object.
An object is moving with constant speed v. The distance S covered by the object is the product of speed v and time t. S = vt
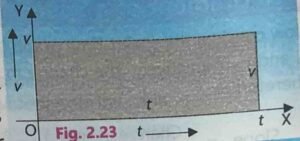
The area under the graph for time interval t is the area of the rectangle of sides t and v.
If t is the length and v is the width of the rectangle, then area of that rectangle will be vt because area of rectangle is equal to the product of length and width.
Area of rectangle = v t
Distance = v t
Hence area of rectangle = distance
Lets check it in case of right angled triangle.
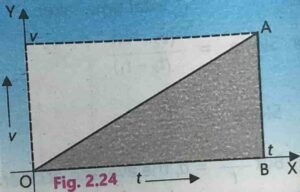
If the speed of an object increases uniformly from 0 to v in time t, then average speed will 1/2 v.
Distance covered = average speed x time
$$S\;=\;\frac12v\;\times\;t$$
Area of right angled triangle is equal to the half of the product of base and perpendicular
Hence area of triangle = distance
Hence the area under the speed-time graph is numerically equal to the distance covered by the object.
————————————————————————————————————————————————–
2.7 How equations of motion can be applied to the bodies moving under the action gravity?
When a body falls freely under the action of gravity of the Earth. acceleration acting on it will be gravitational acceleration denoted by g. So we will replace a by g and due to height distance S by h.
g will be positive in downward direction and negative in the upward direction
$$g\;=\;9.8\;m\;s^{-2}$$
But for our convenience we will use
$$g\;=\;10\;m\;s^{-2}$$
1st equation of motion
$$v_f=v_1+\;a\;t\\\\For\;freely\;falling\;object\\\\v_f=v_1+\;g\;t$$
2nd equation of motion
$$S\;=\;v_i\;t\;+\;\frac12\;a\;t^2\;\\\\For\;freely\;falling\;object\\\\h\;=\;v_i\;t\;+\;\frac12\;g\;t^2$$
3rd equation of motion
$$2\;a\;S\;=\;v_r^2\;-\;v_i^2\\\\For\;freely\;falling\;object\\\\2\;g\;h\;=\;v_r^2\;-\;v_i^2$$
————————————————————————————————————————————————–
Physics 9th New Book Chapter2 Numerical
$$2.1\;\;Draw\;the\;\\representative\;line\;of\\the\;following\;vectors:\\(a)\;A\;velocity\;of\\400\;m\;s^{-1}\;making\;an\\angle\;of\;60\;degree\\with\;x-axis.\\(b)\;A\;force\;of\;50\;N\\making\;an\;angle\;of\\120^\circ\;\;with\;x-axis.$$


====================================================================================
$$2.2\;\;\;A\;car\;is\;moving\\with\;an\;average\;speed\\of\;73\;km\;h^{-1}.\;\;How\\much\;time\;will\;it\\take\;to\;cover\;a\\dis\tan ce\;of\;360\;km\;?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Average\mathit\;speed\mathit\;\mathit=\mathit\;v_{\mathit a\mathit v}\mathit=\mathit\;\mathit{72}\mathit\;km\mathit\;h^{\mathit-\mathit1}\\Distance\mathit\;\mathit=\mathit\;S\mathit\;\mathit=\mathit\;\mathit{360}\mathit\;km\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\;S\;=\;v_{av}\;\times\;t\\\\\mathit{360}\mathit\;km\mathit\;\mathit=\mathit\;\mathit{72}\mathit\;km\mathit\;h^{\mathit-\mathit1}\mathit\;\mathit\times\mathit\;t\\\frac{\mathit{360}\mathit\;\mathit k\mathit m}{\mathit{72}\mathit\;\mathit k\mathit m\mathit\;\mathit h^{\mathit-\mathit1}}\mathit\;\mathit=\mathit\;t\\\mathit5\mathit\;h\mathit\;\mathit=\mathit\;t\\t\mathit\;\mathit=\mathit\;\mathit5\mathit\;h\\$$
====================================================================================
$$2.3\;\;\;A\;truck\;starts\\from\;rest.\;It\;reaches\\a\;velocity\;of\;90\;km\;h^{-1}\\in\;50\;seconds.\;Find\\its\;average\;acceleration.\\$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit{90}\mathit\;km\mathit\;h^{\mathit-\mathit1}\\\\\mathit=\mathit\;\mathit{90}\mathit\;\mathit\times\mathit\;\frac{\mathit{1000}}{\mathit{3600}}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;\mathit{90}\mathit\;\mathit\times\mathit\;\mathit0\mathit.\mathit{277}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\\\\mathit\;\mathit=\mathit\;\mathit{24}\mathit.\mathit{93}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit{50}\mathit\;seconds\\\\Average\mathit\;acceleration\mathit\;\mathit=\mathit\;a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol\;\boldsymbol:\boldsymbol-\\a_{av}\;=\;\;\frac{v_f\;-\;v_i}t\\\\a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit\;\frac{\mathit\;\mathit{24}\mathit.\mathit{93}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}\mathit\;\mathit\;\mathit-\mathit\;\mathit0\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}}{\mathit{50}\mathit\;\mathit s}\\\\a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit\;\frac{\mathit\;\mathit{24}\mathit.\mathit{93}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}}{\mathit{50}\mathit\;\mathit s}\\\\a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit0\mathit.\mathit{498}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\a_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit0\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\\\\\\\\\$$
====================================================================================
$$2.4\;\;A\;car\;passes\;a\\green\;traffic\;signal\\while\;moving\;with\;a\\velocity\;of\;5\;m\;s^{-1}.\\It\;then\;accelerates\;to\\1.5\;m\;s^{-2}.\;What\;is\;the\\velocity\;of\;car\;after\\5\;seconds?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Acceleration\mathit\;\mathit=\mathit\;a\mathit\;\mathit=\mathit\;\mathit1\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit5\mathit\;seconds\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\v_f\;=\;v_i\;+\;at\\\\v_{\mathit f}\mathit=\mathit\;\mathit\;\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit+\mathit\;\mathit1\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit\;\mathit(\mathit5\mathit\;s\mathit)\\\\v_{\mathit f}\mathit=\mathit\;\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit+\mathit\;\mathit7\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\\\v_{\mathit f}\mathit=\mathit\;\mathit{12}\mathit.\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\\\\\\\\\\$$
====================================================================================
$$2.5\;\;A\;motercycle\\initally\;travelling\;at\\18\;km\;h^{-1}\;accelerates\\at\;cons\tan t\;rate\;of\\2\;m\;s^{-2}.\;How\;far\\will\;the\;motercycle\\go\;in\;10\;seconds?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Initial\mathit\;speed\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit{18}\mathit\;km\mathit\;h^{\mathit-\mathit1}\\\\\mathit=\mathit\;\mathit{18}\mathit\;\mathit\times\frac{\mathit{1000}}{\mathit{3600}}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;\mathit{18}\mathit\;\mathit\times\mathit\;\mathit0\mathit.\mathit{278}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\mathit\;\mathit=\mathit\;\mathit5\mathit.\mathit{004}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Acceleration\mathit\;\mathit=\mathit\;a\mathit\;\mathit=\mathit\;\mathit2\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Time\;=\;t\;=\;10\;s\\\\Dis\tan ce\;=\;s\;=\;?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol s\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf i}\boldsymbol\;\boldsymbol t\boldsymbol\;\boldsymbol+\boldsymbol\;\frac{\mathbf1}{\mathbf2}\boldsymbol\;\boldsymbol a\boldsymbol\;\boldsymbol t^{\mathbf2}\\\\s\mathit\;\mathit=\mathit\;\mathit\;\mathit(\mathit5\mathit.\mathit{004}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit)\mathit\;\mathit(\mathit{10}s\mathit)\mathit\;\mathit+\mathit\;\frac{\mathit1}{\mathit2}\mathit\;\mathit(\mathit2\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;{\mathit(\mathit{10}s\mathit)}^{\mathit2}\\\\s\mathit\;\mathit=\mathit\;\mathit{50}\mathit.\mathit{04}\mathit\;m\mathit\;\mathit+\mathit\;\mathit{100}\mathit\;m\\\\s\mathit\;\mathit=\mathit\;\mathit{150}\mathit.\mathit{04}\mathit\;m$$
====================================================================================
$$2.6\;\;A\;wagon\;is\\moving\;on\;a\;road\\with\;a\;velocity\\of\;54\;km\;h^{-1}.\\Brakes\;are\;applied\\suddenly.\;The\;wagon\\covers\;a\;dis\tan ce\;of\\25\;m\;before\;stopping.\\Determine\;the\;\\acceleration\;of\;the\;wagon.$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit{54}\mathit\;km\mathit\;h^{\mathit-\mathit1}\\\\\mathit=\mathit{54}\mathit\;\mathit\times\mathit\;\frac{\mathit{1000}}{\mathit{3600}}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;\mathit{54}\mathit\;\mathit\times\mathit\;\mathit0\mathit.\mathit{278}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\mathit=\mathit\;\mathit{15}\mathit.\mathit{012}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Distance\mathit\;\mathit=\mathit\;S\mathit\;\mathit=\mathit\;\mathit{25}\mathit\;m\\\\Acceleration\mathit\;\mathit=\mathit\;a\mathit\;\mathit=\mathit\;\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\mathbf2\boldsymbol a\boldsymbol S\boldsymbol\;\boldsymbol=\boldsymbol\;{\mathbf v}_{\mathbf f}^{\mathbf2}\boldsymbol\;\boldsymbol-\boldsymbol\;{\mathbf v}_{\mathbf i}^{\mathbf2}\\\\\mathit2a\mathit(\mathit{25}m\mathit)\mathit\;\mathit=\mathit\;\mathit0^{\mathit2}\mathit\;\mathit-\mathit\;{\mathit(\mathit{15}\mathit.\mathit{012}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit)}^{\mathit2}\\\\a\mathit\;\mathit=\mathit\;\frac{\mathit-\mathit{225}\mathit.\mathit{36}\mathit\;\mathit m^{\mathit2}\mathit\;\mathit s^{\mathit-\mathit2}}{\mathit{50}\mathit m}\\\\a\mathit\;\mathit=\mathit\;\mathit-\mathit4\mathit.\mathit{507}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\$$
====================================================================================
$$2.7\;\;A\;stone\;is\;dropped\\from\;a\;height\;of\;45\;m.\\How\;long\;will\;it\;take\;to\\reach\;the\;ground\;?\;What\\will\;be\;its\;velocity\;just\\before\;hitting\;the\;ground\;?\\\\$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Height\mathit\;\mathit=\mathit\;h\mathit\;\mathit=\mathit\;\mathit{45}\mathit\;m\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit?\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol h\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol v{\boldsymbol i}_{\mathbf t}\boldsymbol\;\boldsymbol+\boldsymbol\;\frac{\mathbf1}{\mathbf2}\boldsymbol\;\boldsymbol g\boldsymbol\;\boldsymbol t^{\mathbf2}\\\\\mathit{45}\mathit\;m\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit(t\mathit\;seconds\mathit)\mathit\;\mathit+\frac{\mathit1}{\mathit2}\mathit(\mathit{10}\mathit\;\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;\mathit(t^{\mathit2}\mathit)\\\\\mathit{45}\mathit\;m\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;\mathit+\mathit(\mathit\;\mathit5\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;\mathit(t^{\mathit2}\mathit)\\\\\frac{\mathit{45}\mathit\;\mathit m}{\mathit5\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit2}}\mathit=\mathit\;t^{\mathit2}\\\\\mathit9\mathit\;s^{\mathit2}\mathit\;\mathit=\mathit\;t^{\mathit2}\\\\Taking\mathit\;square\mathit\;root\mathit\;on\mathit\;both\mathit\;side\\\\t\mathit\;\mathit=\mathit\;\mathit3\mathit\;s\\\\$$
$$\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\boldsymbol\;\\{\boldsymbol v}_{\mathbf f}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf i}\boldsymbol\;\boldsymbol+\boldsymbol\;\boldsymbol a\boldsymbol\;\boldsymbol t\\\\v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;\mathit+\mathit\;\mathit(\mathit3\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;\mathit(\mathit{10}s\mathit)\\\\v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}$$
====================================================================================
$$2.8\;\;A\;car\;travels\\10\;km\;with\;an\\average\;velocity\;of\\20\;m\;s^{-1}.\;Then\;it\\travels\;in\;the\;same\\direction\;through\;a\\diversion\;at\;an\\average\;velocity\;of\\4\;m\;s^{-1}\;for\;the\;next\\0.8\;km.\;Determine\;the\\average\;velocity\;of\;the\\car\;for\;the\;total\;journey.$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Distance\mathit\;\mathit=\mathit\;S_{\mathit1}\mathit\;\mathit=\mathit\;\mathit{10}\mathit\;km\mathit\;\mathit=\mathit\;\mathit{10}\mathit\;\mathit\times\mathit\;\mathit{1000}\mathit\;m\\\mathit=\mathit\;\mathit{10000}\mathit\;m\\\\Average\mathit\;velocity\mathit\;\mathit=\mathit\;v{\mathit1}_{\mathit a\mathit v}\mathit=\mathit\;\mathit{20}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\time\mathit\;\mathit=\mathit\;t_{\mathit1}\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\{\boldsymbol S}_{\mathbf1}\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol v{\mathbf1}_{\mathbf a\mathbf v}\boldsymbol\;\boldsymbol\times\boldsymbol\;{\boldsymbol t}_{\mathbf1}\\\\\mathit{10000}\mathit\;m\mathit\;\mathit=\mathit\;\mathit{20}\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit\times\mathit\;\mathit\;t_{\mathit1}\\\\\frac{\mathit{10000}\mathit\;\mathit m}{\mathit{20}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}}\mathit\;\mathit=\mathit\;t_{\mathit1}\\\\t_{\mathit1}\mathit\;\mathit=\mathit\;\mathit{500}\mathit\;s\\\\\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Distance\mathit\;\mathit=\mathit\;S_{\mathit2}\mathit\;\mathit=\mathit\;\mathit0\mathit.\mathit8\mathit\;km\mathit\;\mathit=\mathit\;\mathit0\mathit.\mathit8\mathit\;\mathit\times\mathit\;\mathit{1000}\mathit\;m\\\mathit=\mathit\;\mathit{800}\mathit\;m\\\\Average\mathit\;velocity\mathit\;\mathit=\mathit\;v{\mathit2}_{\mathit a\mathit v}\mathit=\mathit\;\mathit4\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\time\mathit\;\mathit=\mathit\;t_{\mathit2}\mathit\;\mathit=\mathit\;\mathit?\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\{\boldsymbol S}_{\mathbf2}\boldsymbol\;\boldsymbol=\boldsymbol\;\boldsymbol v{\mathbf2}_{\mathbf a\mathbf v}\boldsymbol\;\boldsymbol\times\boldsymbol\;{\boldsymbol t}_{\mathbf2}\\\\\mathit{800}m\mathit\;\mathit=\mathit\;\mathit4\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit\times\mathit\;\mathit\;t_{\mathit2}\\\\\frac{\mathit{800}\mathit\;\mathit m}{\mathit4\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}}\mathit\;\mathit=\mathit\;t_{\mathit2}\\\\\mathit\;t_{\mathit2}\mathit\;\mathit=\mathit\;\mathit{200}\mathit\;s\\\\t\mathit\;\mathit=\mathit\;t_{\mathit1}\mathit\;\mathit+\mathit\;t_{\mathit2}\\\\t\mathit\;\mathit=\mathit\;\mathit{500}\mathit\;m\mathit\;\mathit+\mathit\;\mathit{200}\mathit\;m\\\\t\mathit\;\mathit=\mathit\;\mathit{700}\mathit\;s\\\\\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\\\\Distance\mathit\;\mathit=\mathit\;S\mathit\;\mathit=\mathit?\\\\time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit{700}\mathit\;s\\\\Average\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit?\\\\Distance\mathit\;\mathit=\mathit\;S\mathit\;\mathit=S_{\mathit1}\mathit+\mathit\;S_{\mathit2}\mathit\;\mathit=\mathit\;\mathit{10000}m\mathit+\mathit{800}m\\\mathit=\mathit\;\mathit{10800}m\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\boldsymbol S\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf a\mathbf v}\boldsymbol\;\boldsymbol\times\boldsymbol\;\boldsymbol t\\\\\mathit{10800}\mathit\;m\mathit\;\mathit=\mathit\;v_{\mathit a\mathit v}\mathit\;\mathit\times\mathit\;\mathit{700}\mathit\;s\\\\\frac{\mathit{10800}\mathit\;\mathit m\mathit\;}{\mathit{700}\mathit\;\mathit s}\mathit\;\mathit=\mathit\;\mathit\;v_{\mathit a\mathit v}\\\\\mathit\;v_{\mathit a\mathit v}\mathit\;\mathit=\mathit\;\mathit{15}\mathit.\mathit{428}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\\\\\\$$
====================================================================================
$$2.9\;\;A\;ball\;is\;dropped\\from\;the\;top\;of\;a\\tower.\;The\;ball\\reaches\;the\;ground\\in\;5\;seconds.\;Find\\height\;of\;the\;tower\;\\and\;velocity\;of\;the\\ball\;with\;which\;it\\strikes\;the\;ground.\;$$
$$\;\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol:\boldsymbol-\boldsymbol\;\\\\Time\mathit\;\mathit=\mathit\;\mathit5\mathit\;seconds\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Gravitional\mathit\;accelerational\mathit\;\mathit=\mathit\;g\mathit\;\mathit=\mathit\;\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Height\mathit\;\mathit=\mathit\;h\mathit\;\mathit=\mathit\;\mathit?\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\boldsymbol h\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol v}_{\boldsymbol i}\boldsymbol{\mathit\;}\boldsymbol t\boldsymbol{\mathit\;}\boldsymbol{\mathit+}\boldsymbol{\mathit\;}\frac{\boldsymbol1}{\boldsymbol2}\boldsymbol{\mathit\;}\boldsymbol g\boldsymbol{\mathit\;}\boldsymbol t^{\boldsymbol2}\\\\h\;=\;(0\;m\;s^{-1})\;(5\;s)\;+\;\frac12\;(10\;m\;s^{-2})\;{(5\;s)}^2\\\\h\;=\;0\;m\;+\;125\;m\\\\h\;=\;125\;m\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\{\boldsymbol v}_{\mathbf f}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol v}_{\mathbf i}\boldsymbol\;\boldsymbol+\boldsymbol\;\boldsymbol g\boldsymbol\;\boldsymbol t\\\\\\v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit+\mathit\;\mathit(\mathit\;\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;\mathit(\mathit\;\mathit5\mathit\;s\mathit\;\mathit)\\\\v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit+\mathit\;\mathit{50}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit{50}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\\\\\\\\\\$$
====================================================================================
$$2.10\;\;A\;cricket\;ball\\is\;hit\;so\;that\;it\\travels\;straight\;up\\in\;the\;air.\;An\\observer\;notes\;that\\it\;took\;3\;seconds\\to\;reach\;the\;highest\\point.\;What\;was\;the\\initial\;velocity\;of\;the\\ball\;?\;If\;the\;ball\;was\\hit\;1\;m\;above\;the\\ground,\;how\;high\;did\\it\;rise\;from\;\;the\;ground\;?$$
$$\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\Time\mathit\;\mathit=\mathit\;t\mathit\;\mathit=\mathit\;\mathit3\mathit\;seconds\\\\Gravitional\mathit\;acceleration\mathit\;\mathit=\mathit\;g\mathit\;\mathit=\mathit\;\mathit-\mathit\;\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\{\boldsymbol v}_{\boldsymbol f}\boldsymbol{\mathit\;}\boldsymbol{\mathit=}\boldsymbol{\mathit\;}{\boldsymbol v}_{\boldsymbol i}\boldsymbol{\mathit\;}\boldsymbol{\mathit+}\boldsymbol{\mathit\;}\boldsymbol g\boldsymbol{\mathit\;}\boldsymbol t\\\\\\\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit+\mathit\;\mathit(\mathit\;\mathit-\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit)\mathit\;\mathit(\mathit\;\mathit3\mathit\;s\mathit\;\mathit)\\\\\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit\;\mathit-\mathit\;\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\\\\boldsymbol D\boldsymbol a\boldsymbol t\boldsymbol a\boldsymbol{\mathit:}\boldsymbol{\mathit-}\\\\\\Initial\mathit\;height\mathit\;\mathit=\mathit\;h_{\mathit1}\mathit\;\mathit=\mathit\;\mathit1\mathit\;m\\\\Initial\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit i}\mathit\;\mathit=\mathit\;\mathit{30}\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Final\mathit\;velocity\mathit\;\mathit=\mathit\;v_{\mathit f}\mathit\;\mathit=\mathit\;\mathit0\mathit\;m\mathit\;s^{\mathit-\mathit1}\\\\Gravitional\mathit\;acceleration\mathit\;\mathit=\mathit\;g\mathit\;\mathit=\mathit\;\mathit-\mathit\;\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\\\\Height\mathit\;\mathit=\mathit\;h_{\mathit2}\mathit\;\mathit=\mathit\;\mathit?\\\\Total\mathit\;height\mathit\;\mathit=\mathit\;h\mathit\;\mathit=\mathit?\\\\\\\boldsymbol F\boldsymbol o\boldsymbol r\boldsymbol m\boldsymbol u\boldsymbol l\boldsymbol a\boldsymbol:\boldsymbol-\\\mathbf2\boldsymbol g{\boldsymbol h}_{\mathbf2}\boldsymbol\;\boldsymbol=\boldsymbol\;{\boldsymbol({\boldsymbol v}_{\mathbf f}\boldsymbol)}^{\mathbf2}\boldsymbol\;\boldsymbol-\boldsymbol\;{\boldsymbol({\mathbf v}_{\mathbf i}\boldsymbol)}^{\mathbf2}\\\\\\\mathit2\mathit\;\mathit(\mathit\;\mathit-\mathit\;\mathit{10}\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit\;\mathit)\mathit\;h_{\mathit2}\mathit\;\mathit=\mathit\;\mathit\;{\mathit(\mathit\;\mathit0\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}\mathit)}^{\mathit2}\mathit\;\mathit-\mathit\;{\mathit(\mathit{30}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}\mathit)}^{\mathit2}\\\\\mathit\;\mathit(\mathit\;\mathit-\mathit\;\mathit{20}\mathit\;m\mathit\;s^{\mathit-\mathit2}\mathit\;\mathit)\mathit\;h_{\mathit2}\mathit\;\mathit=\mathit\;\mathit-\mathit\;{\mathit(\mathit{30}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit1}\mathit)}^{\mathit2}\\\\h_{\mathit2}\mathit\;\mathit=\mathit\;\frac{\mathit{900}\mathit\;\mathit m^{\mathit2}\mathit\;\mathit s^{\mathit-\mathit2}}{\mathit{20}\mathit\;\mathit m\mathit\;\mathit s^{\mathit-\mathit2}}\\\\h_{\mathit2}\mathit\;\mathit=\mathit\;\mathit{45}\mathit\;m\\\\h\mathit\;\mathit=\mathit\;h_{\mathit1}\mathit\;\mathit+\mathit\;h_{\mathit2}\\\\h\mathit\;\mathit=\mathit\;\mathit1m\mathit\;\mathit+\mathit\;\mathit{45}m\\\\h\mathit\;\mathit=\mathit\;\mathit{46}m\\\\\\\\\\\\\\\\\\\\\\\\\\$$
Check! Some useful links below.




